2021年广东省深圳市二十三校联考九年级下学期第二次教学质量检测数学试卷(二模)试题
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 下列四个数:-3,-0.8, , 中,绝对值最小的是( )A、-3 B、-0.8 C、 D、
-
2. 如图所示的几何体的俯视图为( )
 A、
A、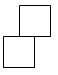 B、
B、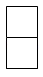 C、
C、 D、
D、
-
3. 在国家大数据战略的引领下,我国在人工智能领域取得显著成就,自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军,这得益于所建立的大数据中心的规模和数据存储量,它们决定着人工智能深度学习的质量和速度,其中的一个大数据中心能存储58000000000本书籍,将58000000000用科学记数法表示应为( )A、 B、 C、 D、
-
4. 在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
5. 如果一个正多边形的内角和等于1080°,那么该正多边形的一个外角等于( )A、30° B、45° C、60° D、72°
-
6. 下列命题中:①长度相等的弧是等弧;②有一个角对应相等的两个等腰三角形相似;③对角线互相垂直平分的四边形是正方形;④有两边及一角对应相等的两个三角形全等,真命题的个数是( )A、3 B、2 C、1 D、0
-
7. 如图,和都是等腰直角三角形, , 反比例函数在第一象限的图象经过点 , 则和的面积之差为( )
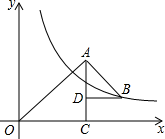 A、 B、 C、 D、
A、 B、 C、 D、 -
8. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
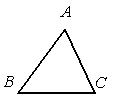 A、
A、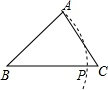 B、
B、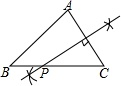 C、
C、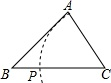 D、
D、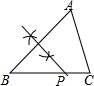
-
9. 如图,在边长为1的小正方形网格中,点、、、都在这些小正方形的顶点上,AB、OD相交于点O,则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=45°;③CE=2DE;④AG∥CF;⑤S△FGC= .其中正确结论的个数是( )
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个
二、填空题
-
11. 分解因式:3x2-6x+3= .
-
12. 已知一组数据x1 , x2 , x3 , x4的方差是2,则数据x1+5,x2+5,x3+5,x4+5的方差是 .
-
13. 如图,一次函数的图象与反比例函数的图象交于、两点,则不等式的解集为 .

-
14. 如图所示,抛物线 与x轴交于A、B两点,过点B的直线与抛物线交于点C(点C在x轴上方),过ABC三点的⊙M满足∠MBC=45°,则点C的坐标为.
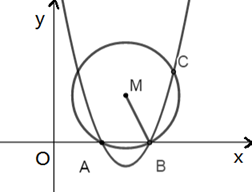
-
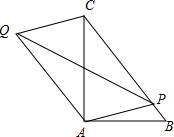
15. 如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为.
三、解答题
-
16. 计算: .
-
17. 荆车中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动.为了了解学生对这四种活动的喜爱情况,学校随机调查了该校
 名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图. (1)、
(1)、 ,
,  ; (2)、请补全上图中的条形图;(3)、根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱足球;(4)、在抽查的
; (2)、请补全上图中的条形图;(3)、根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱足球;(4)、在抽查的 名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率. -
18. 在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕点旋转一定角度.研究表明:当眼睛E与显示屏顶端在同一水平线上,且望向显示器屏幕形成一个18°俯角,即望向屏幕中心的视线与水平线的夹角时,对保护眼睛比较好,而且显示屏顶端与底座的连线与水平线垂直时(如图2)时,观看屏幕最舒适,此时测得 , , 液晶显示屏的宽为 .
 (1)、求眼睛与显示屏顶端的水平距离AE.(结果精确到)(2)、求显示屏顶端与底座的距离 . (结果精确到)(参考数据: , , , , )
(1)、求眼睛与显示屏顶端的水平距离AE.(结果精确到)(2)、求显示屏顶端与底座的距离 . (结果精确到)(参考数据: , , , , ) -
19. 如图,在中, , 为中点, , 且 .
 (1)、求证:四边形AEBD是矩形;(2)、连接CE交AB于点 , 若 , , 求的长.
(1)、求证:四边形AEBD是矩形;(2)、连接CE交AB于点 , 若 , , 求的长. -
20. 某社区拟建 , 两类摊位以搞活“地摊经济”,每个 类摊位的占地面积比每个 类摊位的占地面积多2平方米,建 类摊位每平方米的费用为40元,建 类摊位每平方米的费用为30元,用60平方米建 类摊位的个数恰好是用同样面积建 类摊位个数的 .(1)、求每个 , 类摊位占地面积各为多少平方米?(2)、该社拟建 , 两类摊位共90个,且 类摊位的数量不少于 类摊位数量的3倍.求建造这90个摊位的最大费用.
-
21. 已知AB为的直径,为上一动点,连接 , , 在BA的延长线上取一点D,连接 , 使 .
 (1)、如图1,若 , 求证:CD是的切线;(2)、如图2,延长交于点E,连接AE.
(1)、如图1,若 , 求证:CD是的切线;(2)、如图2,延长交于点E,连接AE.①若的直径为 , , 求AD的长;
②若 , 求的值.
-
22. 如图,抛物线 与 轴交于点 和点 ,与y轴交于点C,连接 ,点P是线段 上的动点(与点 不重合),连接 并延长 交抛物线于点Q,连接 ,设点Q的横坐标为m.
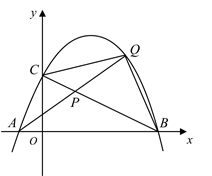 (1)、求抛物线的解析式和点C的坐标;(2)、当 的面积等于2时,求m的值;(3)、在点P运动过程中, 是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
(1)、求抛物线的解析式和点C的坐标;(2)、当 的面积等于2时,求m的值;(3)、在点P运动过程中, 是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
