2021年广东省深圳市宝安区中考数学模拟试卷（一）

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、2 B、±2 C、16 D、±16

查看试题解析
2. 下列四个图案分别是厨余垃圾、可回收物、有害垃圾、其他垃圾的标识，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 2021年3月20日至29日，“2021粤港澳大湾区深圳花展”将在深圳仙湖植物园开幕，届时将有7.1万m²的绝美花海，19个国家，5大主题，38座花园供游客欣赏．数据7.1万m²用科学记数法表示为（）

A、71×10⁴m² B、7.1×10⁴m² C、7.1×10⁵m² D、0.71×10⁵m²

查看试题解析
4. 为了增强学生预防新冠肺炎的安全意识，某校开展疫情防控知识竞赛．来自不同年级的30名参赛同学的得分情况如下表所示，这些成绩的中位数和众数分别是（）

成绩/分

84

88

92

96

100

人数/人

2

4

9

10

5

A、92分，96分 B、94分，96分 C、96分，96分 D、96分，100分

查看试题解析
5. 一个多边形的内角和是外角和的2倍，这个多边形是（）

A、四边形 B、五边形 C、六边形 D、八边形

查看试题解析
6. 天虹商场购将两件商品清仓销售，售价均为120元，其中一件商品获利20%，另一件商品亏损20%，则天虹商场销售完这两件商品的盈亏情况为（）

A、盈利10元 B、亏损10元 C、不盈不亏 D、无法确定

查看试题解析
7. 如图， $R t △ A B C$ 中， $∠ A B C = 90 °$ ，根据尺规作图的痕迹判断以下结论不正确的是（）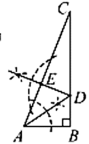

A、 $D B = D E$ B、 $A B = A E$ C、 $∠ E D C = ∠ B A C$ D、 $∠ D A C = ∠ C$

查看试题解析
8. 如果一个正整数能表示为两个正整数的平方差，那么这个正整数就称为“智慧数”，例如：5＝3²﹣2² ， 5就是一个智慧数，则下列各数不是智慧数的是（）

A、2020 B、2021 C、2022 D、2023

查看试题解析
9. 如图，抛物线y＝ax²+bx+c（a≠0）对称轴为直线x＝﹣1，则下列结论不正确的是（）

A、abc＞0 B、4a﹣2b+c＞0 C、3b+2c＜0 D、m（am+b）+b＜a（m是任意实数）

查看试题解析
10. 如图，正方形ABCD中，AC与BD交于点O，M是对角线AC上的一个动点，直线BM与直线AD交于点E，过A作AH垂直BE于点H，直线AH与直线BD交于点N，连接EN、OH，则下列结论：①BM＝AN；②OH平分∠MHN；③当EN∥OM时，BN²＝DN•DB；④当M为AO中点时， $\frac{A H}{B M}$ ＝ $\frac{2}{5}$ ，正确结论的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解：a（a﹣b）﹣b（b﹣a）＝．

查看试题解析
12. 有五张背面相同的卡片，正面分别印有圆、矩形、等边三角形、菱形、平行四边形，现将五张卡片正面朝下洗匀任意摆放，从中随机抽取一张，抽到的卡片恰好是中心对称图形的概率为．

查看试题解析
13. 如图，在菱形ABCD中，∠A＝60°，E为AD边上的一个动点，连接BE，将AB沿着BE折叠得到A'B，A的对应点为A'，连接A'D，当A′B⊥AD时，∠A'DE的度数为．

查看试题解析
14. 如图，点A，B，C，D在正方形网格的格点上，连接AB、CD交于点P，则tan∠APC＝．

查看试题解析
15. 如图，直线 $y = - \frac{4}{3} x + 4$ 与x轴、y轴分别交于C、D两点，点B为线段OD上的一个动点（不与O、D重合），点B关于直线CD的对称点B′恰好落在反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上，连接CB，CB′，BB′，B′D，当tan∠CBB'＝2时，k的值为．

查看试题解析

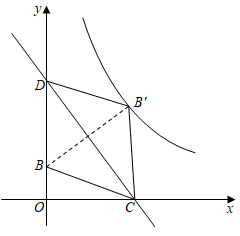
三、解答题

16. 计算： $(2020 - π)^{0} - | 2 - \sqrt{3} | + \sqrt{3} t a n 4 5^{°} + (- \frac{1}{3})^{- 1}$ ．

查看试题解析
17. 解不等式组 ${\begin{array}{l} 2 x - 4 < x - 1 \\ \frac{3 x - 4}{6} \leq \frac{2 x - 1}{3} \end{array}$ ，并利用数轴确定不等式组的解集．

查看试题解析
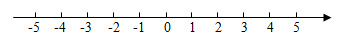18. 某校对八年级学生进行一次垃圾分类知识竞赛，成绩x分（x为整数）评定为优秀、良好、合格、不合格四个等级（优秀、良好、合格、不合格分别用A、B、C、D表示），A等级：90≤x≤100，B等级：80≤x＜90，C等级：60≤x＜80，D等级：0≤x＜60．该校随机抽取了一部分学生的成绩进行调查，并绘制不完整的统计图表．
等级
频数（人数）
频率
A
a
20%
B
16
40%
C
b
m
D
4
10%
请你根据统计图表提供的信息解答下列问题：

(1)、上表中的a＝， b＝， m＝．

(2)、本次调查共抽取了 ▲ 名学生．请补全条形图．

(3)、若从D等级的4名学生中抽取两名学生进行问卷调查，请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率．

查看试题解析
19. 如图，在△ABC中，AB=AC，点D是BC的中点，点E是AD的中点，延长BE至F，使EF=BE，连接AF、CF、BF与AC交于点 G．

(1)、求证：四边形ADCF 是矩形；

(2)、若AB=5，BC=6，线段CG 的长为．

查看试题解析
20. 为了抗击“新型肺炎”，我市某医药器械厂接受了生产一批高质量医用口罩的任务，任务要求在30天之内（含30天）生产A型和B型两种型号的口罩共200万只．在实际生产中，由于受条件限制，该工厂每天只能生产一种型号的口罩．已知该工厂每天可生产A型口罩的个数是生产B型口罩的2倍，并且加工生产40万只A型口罩比加工生产50万只B型口罩少用6天．

(1)、该工厂每天可加工生产多少万只B型口罩？

(2)、若生产一只A型口罩的利润是0.8元，生产一只B型口罩的利润是1.2元，在确保准时交付的情况下，如何安排工厂生产可以使生产这批口罩的利润最大？

查看试题解析
21. 如图1，等腰△ABC内接于⊙O，AC＝BC，CD⊥AB于点D，F为弧AB上的一个动点，连接CF交AB于点G，P为射线AB上的一个动点，连接PF，AF．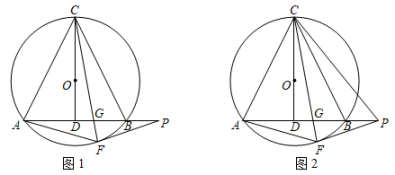

(1)、求证：CF•CG＝CA²；

(2)、如图1，若PG＝PF，求证：PF为⊙O的切线；

(3)、在（2）的条件下，如图2，连接PC，若∠FAP＝∠PCB，AB＝CD＝4，求 $\frac{1}{B G} - \frac{1}{B P}$ 的值．

查看试题解析
22. 如图，二次函数y＝ax²+5ax+7与x轴交于A、C两点，与y轴交于B点，若OB：OC＝7：2．点P是抛物线第二象限内的一个动点．连接PC交y轴于点D，连接PB．

(1)、求抛物线的解析式；

(2)、如图1，设P点横坐标为t，△PBD的面积为S，求S与t的关系式；

(3)、如图2，作PE⊥x轴于E，连接ED，点F为ED上一个动点，连接AF交PE于点F，若2∠GAO+∠EDO＝90°，DF＝2EG，求P点坐标．

查看试题解析

成绩/分	84	88	92	96	100
人数/人	2	4	9	10	5

等级	频数（人数）	频率
A	a	20%
B	16	40%
C	b	m
D	4	10%