2021年广东省韶关市中考数学一模试卷

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 在实数﹣3，2，0，﹣4中，最大的数是（）

A、﹣3 B、2 C、0 D、﹣4

查看试题解析
2. 防疫工作一刻都不能放松，截至2021年4月4日22时，全球累计确诊感染新冠肺炎约为1.3亿人，将数字130000000用科学记数法表示为（）．

A、 $0.13 \times 1 0^{9}$ B、 $1.3 \times 1 0^{7}$ C、 $1.3 \times 1 0^{8}$ D、 $1.3 \times 1 0^{9}$

查看试题解析
3. 改革开放以来，我国众多科技实体在各自行业取得了举世瞩目的成就，大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表．上述四个企业的标志是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图是由4个相同的正方体组成的立体图形，它的左视图是（）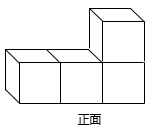

A、 B、 C、 D、

查看试题解析
5. 数据10，11，12，13，14的方差是（）．

A、3 B、25 C、24 D、2

查看试题解析
6. 已知 $∠ A = 53 °$ ，则 $∠ A$ 的余角为（）．

A、47 B、127 C、37° D、147°

查看试题解析
7. 下列运算正确的是（　　）

A、a+2a＝3a² B、a²•a³＝a⁵ C、（ab）³＝ab³ D、（﹣a³）²＝﹣a⁶

查看试题解析
8. 关于x的一元二次方程x²+8x+q=0有两个不相等的实数根，则q的取值范围是（）

A、q<16 B、q>16 C、q≤4 D、q≥4

查看试题解析
9. 直线y=kx+b经过一、二、四象限，则k、b应满足（）

A、k＞0，b＜0 B、k＞0，b＞0 C、k＜0，b＜0 D、k＜0，b＞0

查看试题解析
10. 如图，在正方形 $A B C D$ 中，点E、 $F$ 分别是BC、CD的中点，DE、AF交于点 $G$ ，则下列结论：① $D E ⊥ A F$ ；② $D E = A F$ ；③ $\frac{D F}{A F} = \frac{D G}{A D}$ ；④ $\frac{D F}{A D} = \frac{D G}{G F}$ ，其中正确结论的序号有（）．

A、①②③ B、①② C、①②③④ D、③④

查看试题解析

二、填空题

11. 分解因式： $m^{2} - 4 m + 4 =$ ．

查看试题解析
12. 菱形两条对角线长为8cm和6cm，则菱形面积为cm² ．

查看试题解析
13. 若 $m^{2} + 2 m = 1$ ，则 $4 m^{2} + 8 m - 3$ 的值是．

查看试题解析
14. 按规律排列的一列数： $- \frac{1}{2}$ ， $\frac{2}{5}$ ， $- \frac{3}{8}$ ， $\frac{4}{11}$ ， $- \frac{5}{14}$ ， …，则第2021个数是．

查看试题解析
15. 已知圆锥的底面半径为4cm，高为3cm，则这个圆锥的侧面积为 cm²

查看试题解析
16. 如图为二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象，则下列说法：① $a > 0$ ；② $2 a + b = 0$ ；③ $a + b + c > 0$ ；④ $b^{2} - 4 a c < 0$ ，其中正确的为．（填序号）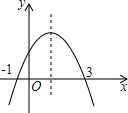

查看试题解析
17. 如图，在四边形 $A B C D$ 中， $A B = C B ， A D = C D$ ．若 $∠ A B D = ∠ A C D = 30 ° ， A D = 1$ ，则 $△ A B C$ 的内切圆面积（结果保留 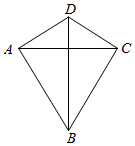$π$ ）．

查看试题解析

三、解答题

18. 计算： ${(\sqrt{2})}^{0} + \sqrt{12} - t a n 60 ° + {(\frac{1}{3})}^{- 2}$

查看试题解析
19. 解分式方程： $\frac{x - 3}{x - 2} + 1 = - \frac{3}{x - 2}$

查看试题解析
20. 如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线.

(1)、用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）

(2)、设DN与AM交于点F，判断△ADF的形状.（只写结果）

查看试题解析
21. 某中学九（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：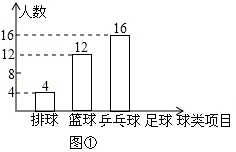

(1)、九（1）班的学生人数为 ▲ ，并把条形统计图补充完整；

(2)、扇形统计图中m= ， n= ，表示“足球”的扇形的圆心角是度；

(3)、排球兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的排球队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．

查看试题解析
22. 如图，一次函数 $y = - x + 6$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限的图象交于 $A (1 ， m)$ 和B两点，与x轴交于点C，连接 $O A ， O B .$

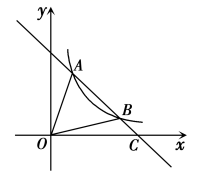(1)、求反比例函数的解析式；

(2)、若点P在x轴上，且 $S_{△ A P C} = \frac{1}{2} S_{△ O A B}$ ，求点P的坐标.

查看试题解析
23. 戴口罩可以有效降低感染新型冠状病毒的风险．某学校在本学期开学初为九年级学生购买A、B两种口罩，经过市场调查，A的单价比B的单价少2元，购买150个A口罩和购买90个B口罩的费用相等．

(1)、求 $A$ 、 $B$ 两种口罩的单价；

(2)、若学校需购买两种口罩共500个，总费不超过2100元，求该校本次购买 $A$ 种口罩最少有多少个？

查看试题解析
24. 如图，AC为⊙O的直径，B为AC延长线上一点，且∠BAD＝∠ABD＝30°，BC＝1，AD为⊙O的弦，连接BD，连接DO并延长交⊙O于点E，连接BE交⊙O于点M．

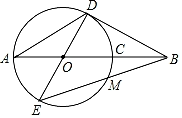(1)、求证：直线BD是⊙O的切线；

(2)、求⊙O的半径OD的长；

(3)、求线段BM的长．

查看试题解析
25. 已知抛物线y＝a $x^{2}$ ＋bx﹣4经过点A（2，0）、B（﹣4，0），与y轴交于点C．

(1)、求这条抛物线的解析式；

(2)、如图1，点P是第三象限内抛物线上的一个动点，当四边形ABPC的面积最大时，求点P的坐标；

(3)、如图2，线段AC的垂直平分线交x轴于点E，垂足为D，M为抛物线的顶点，在直线DE上是否存在一点G，使△CMG的周长最小？若存在，求出点G的坐标；若不存在，请说明理由．

查看试题解析