2021年广东省汕头市濠江区中考数学一模试卷
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 在 , -3,0,5这四个数中,最小的数是( )A、 B、-3 C、0 D、52. 下列是有关防疫的图片,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2020年7月23日,中国首颗火星探测器“天问一号”顺利升空,当“天问一号”探测器抵达火星附近时,总飞行里程将达到470000000公里.470000000这个数字用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、a2+a2=a4 B、a2•a3=a6 C、(a2)3=a5 D、(ab)2=a2b25. 已知一组数据:2,5, ,7,9的平均数是6,则这组数据的众数是( ).A、9 B、7 C、5 D、26. 下列尺规作图,能判断AD是△ABC边上的高是( )
3. 2020年7月23日,中国首颗火星探测器“天问一号”顺利升空,当“天问一号”探测器抵达火星附近时,总飞行里程将达到470000000公里.470000000这个数字用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、a2+a2=a4 B、a2•a3=a6 C、(a2)3=a5 D、(ab)2=a2b25. 已知一组数据:2,5, ,7,9的平均数是6,则这组数据的众数是( ).A、9 B、7 C、5 D、26. 下列尺规作图,能判断AD是△ABC边上的高是( )
A、 B、
B、 C、
C、 D、
D、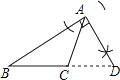 7. 不等式组的解集在数轴上表示为( )A、
7. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 8. 如图,直线 经过点 , ,则不等式 的解集是( )
8. 如图,直线 经过点 , ,则不等式 的解集是( ) A、 B、 C、 D、9. 如图,CD是 的边 上的中线,将线段 绕点D顺时针旋转 后,点A的对应点E恰好落在AC边上,若 ,则 的长为( )
A、 B、 C、 D、9. 如图,CD是 的边 上的中线,将线段 绕点D顺时针旋转 后,点A的对应点E恰好落在AC边上,若 ,则 的长为( ) A、 B、 C、 D、10. 如图,在等边三角形ABC中,点P是BC边上一动点(不与点B,C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是( )
A、 B、 C、 D、10. 如图,在等边三角形ABC中,点P是BC边上一动点(不与点B,C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是( )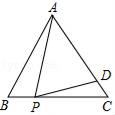 A、
A、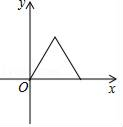 B、
B、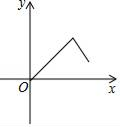 C、
C、 D、
D、
二、填空题
-
11. 分式方程 = 的解是 .12. 分解因式:a2﹣4b2=13. 若 , 则代数式的值为 .14. 如图,将一副三角尺按如图所示的方式叠放(两条直角边重合),则的度数是 .
 15. 若 , 则以的值为边数的多边形的内角和为 .16. 如图,四边形是平行四边形,以点为圆心,为半径的⊙O与相切于点 , 的延长线交⊙O于点 , 连接 , 若 , 则图中阴影的面积为 .
15. 若 , 则以的值为边数的多边形的内角和为 .16. 如图,四边形是平行四边形,以点为圆心,为半径的⊙O与相切于点 , 的延长线交⊙O于点 , 连接 , 若 , 则图中阴影的面积为 . 17. 在△ABC中,∠A=45°,∠B=60°,AB=4,点P、M、N分别在边AB、BC、CA上,连接PM、MN,NP,则△PMN周长的最小值为 .
17. 在△ABC中,∠A=45°,∠B=60°,AB=4,点P、M、N分别在边AB、BC、CA上,连接PM、MN,NP,则△PMN周长的最小值为 .
三、解答题
-
18. 计算:;19. 先化简,再求值: , 其中a=2, .20. “校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
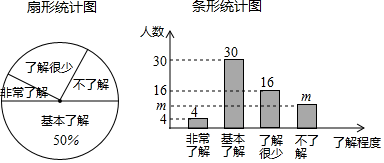 (1)、接受问卷调查的学生共有人,条形统计图中m的值为;(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为;(3)、若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为人;(4)、若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.21. 课间,小明拿着老师的等腰三角板玩,不小心掉在两墙之间,如图所示:
(1)、接受问卷调查的学生共有人,条形统计图中m的值为;(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为;(3)、若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为人;(4)、若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.21. 课间,小明拿着老师的等腰三角板玩,不小心掉在两墙之间,如图所示: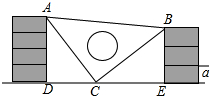 (1)、求证:;(2)、假设砌墙所用的每块砖块的厚度相同,请你帮小明求出的值.22. 某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)、求证:;(2)、假设砌墙所用的每块砖块的厚度相同,请你帮小明求出的值.22. 某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)、求该种商品每次降价的百分率;(2)、若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?
23. 如图,在△ACB中,∠C=90°,AB=2BC,点O在边AB上,且 , 以O为圆心,OB长为半径的圆分别交AB,BC于D,E两点. (1)、求证:AC是⊙O的切线;(2)、判断由D,O,E及切点所构成的四边形的形状,并说明理由.24. 如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
(1)、求证:AC是⊙O的切线;(2)、判断由D,O,E及切点所构成的四边形的形状,并说明理由.24. 如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C. (1)、求抛物线的解析式;(2)、在(1)中抛物线的对称轴是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标,若不存在,请说明理由.(3)、如图2,若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求此时E点的坐标.25. 如图1,平面直角坐标系xOy中,A(4,3),反比例函数 (k>0)的图象分别交矩形ABOC的两边AC,AB于E、F两点(E、F不与A重合),沿着EF将矩形ABOC折叠使A、D两点重合.
(1)、求抛物线的解析式;(2)、在(1)中抛物线的对称轴是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标,若不存在,请说明理由.(3)、如图2,若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求此时E点的坐标.25. 如图1,平面直角坐标系xOy中,A(4,3),反比例函数 (k>0)的图象分别交矩形ABOC的两边AC,AB于E、F两点(E、F不与A重合),沿着EF将矩形ABOC折叠使A、D两点重合. (1)、AE=(用含有k的代数式表示);(2)、如图2,当点D恰好落在矩形ABOC的对角线BC上时,求CE的长度;(3)、若折叠后,△ABD是等腰三角形,求此时点D的坐标.
(1)、AE=(用含有k的代数式表示);(2)、如图2,当点D恰好落在矩形ABOC的对角线BC上时,求CE的长度;(3)、若折叠后,△ABD是等腰三角形,求此时点D的坐标.