2021年广东省汕头市潮南区中考数学模拟试卷
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 的算术平方根为( )A、13 B、±13 C、 D、2. 已知两条线段a=2cm,b=3.5cm,下列线段中能和a,b构成三角形的是( )A、5.5cm B、3.5cm C、1.3cm D、1.5cm3. 随着国家卫健委发布了《新冠疫苗接种技术指南(第一版)》,这意味着新冠疫苗的接种正式向大众开放.据报道,截止2021年4月8日,我国各地累计接种新冠疫苗约14900万剂,把数字14900万用科学记数法表示为( )A、 B、 C、 D、4. 下列图形中,既是中心对称图形,也是轴对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 科克曲线
C、
科克曲线
C、 河图幻方
D、
河图幻方
D、 谢尔宾斯基三角形
5. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作▱BCDE,则∠E的度数为( )
谢尔宾斯基三角形
5. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作▱BCDE,则∠E的度数为( ) A、40° B、50° C、60° D、70°6. 若式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、7. 在平面直角坐标系中,若点 在第三象限,则点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 现有一组数据分别是5、4、6、5、4、13、5,关于这组数据下列说法正确的是( )A、中位数是4 B、众数是7 C、中位数和众数都是5 D、中位数和平均数都是59. 某工厂生产空气净化器,实际平均每天比原计划多生产100台空气净化器,实际生产1200台空气净化器的时间与原计划生产900台空气净化器所需时间相同.若设原计划每天生产台空气净化器,则根据题意可列方程为( )A、 B、 C、 D、10.
A、40° B、50° C、60° D、70°6. 若式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、7. 在平面直角坐标系中,若点 在第三象限,则点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 现有一组数据分别是5、4、6、5、4、13、5,关于这组数据下列说法正确的是( )A、中位数是4 B、众数是7 C、中位数和众数都是5 D、中位数和平均数都是59. 某工厂生产空气净化器,实际平均每天比原计划多生产100台空气净化器,实际生产1200台空气净化器的时间与原计划生产900台空气净化器所需时间相同.若设原计划每天生产台空气净化器,则根据题意可列方程为( )A、 B、 C、 D、10.如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数大致图象是( )
 A、
A、 B、
B、 C、
C、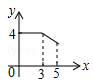 D、
D、
二、填空题
-
11. 因式分解: .12. 已知抛物线与轴的一个交点为 , 则 .13. 不等式组 的解集是 .14. 如图,在中,点、分别在边、上, , 如果 , , 那么的长是 .
 15. 一艘邮轮从港口 处出发,沿北偏东 方向行驶200海里到 港口,卸货后向正南方向行驶到 港口,此时 港口在邮轮的北偏西 方向上,这时邮轮与港口 相距海里.(保留根号)
15. 一艘邮轮从港口 处出发,沿北偏东 方向行驶200海里到 港口,卸货后向正南方向行驶到 港口,此时 港口在邮轮的北偏西 方向上,这时邮轮与港口 相距海里.(保留根号)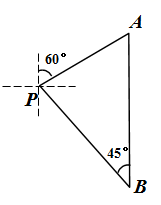 16. 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(﹣1,2),将△AOB绕点A顺时针旋转90°,点O的对应点D恰好落在双曲线y= 上,则k的值为 .
16. 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(﹣1,2),将△AOB绕点A顺时针旋转90°,点O的对应点D恰好落在双曲线y= 上,则k的值为 .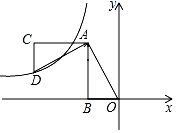 17. 如图,直线l为y= x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1 , 以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2 , 以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为().
17. 如图,直线l为y= x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1 , 以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2 , 以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为().
三、解答题
-
18. 计算:19. 先化简,再求值: ,其中a满足 .20. 如图,△ABC中,BC>AC,∠C=50°.
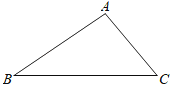 (1)、作图:在CB上截取CD=CA,连接AD,过点D作DE⊥AC,垂足为E;(要求:尺规作图,保留作图痕迹,不写作法)(2)、求∠ADE的度数.21. 根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展“一带一盔”安全守护行动,其中就要求骑行摩托车、电动车需要佩戴头盔.某日我市交警部门在某个十字路口共拦截了50名不带头盔的骑行者,根据年龄段和性别得到如下表的统计信息,根据表中信息回答下列问题:
(1)、作图:在CB上截取CD=CA,连接AD,过点D作DE⊥AC,垂足为E;(要求:尺规作图,保留作图痕迹,不写作法)(2)、求∠ADE的度数.21. 根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展“一带一盔”安全守护行动,其中就要求骑行摩托车、电动车需要佩戴头盔.某日我市交警部门在某个十字路口共拦截了50名不带头盔的骑行者,根据年龄段和性别得到如下表的统计信息,根据表中信息回答下列问题:年龄 (岁)
人数
男性占比
4
50%
60%
25
60%
8
75%
3
100%
(1)、统计表中 的值为;(2)、若要按照表格中各年龄段的人数来绘制扇形统计图,则年龄在“ ”部分所对应扇形的圆心角的度数为;(3)、在这50人中女性有人;(4)、若从年龄在“ ”的4人中随机抽取2人参加交通安全知识学习,请用列表或画树状图的方法,求恰好抽到2名男性的概率.22. 如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,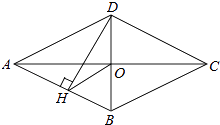 (1)、求证:∠DHO=∠DCO.(2)、若OC=4,BD=6,求菱形ABCD的周长和面积.23. 某商店购进一批清洁剂,每瓶进价为20元,出于营销考虑,要求每瓶清洁剂的售价不低于20元且不高于28元,在销售过程中发现该清洁剂每周的销售量(瓶)与每瓶清洁剂的售价(元)之间满足一次函数关系:当销售单价为22元时,销售量为36瓶;当销售单价为24元时,销售量为32瓶.(1)、求出与的函数关系式,并写出的取值范围;(2)、设该商店每周销售这种清洁剂所获得的利润为元,将该清洁剂销售单价定为多少元时,才能使商店销售该清洁剂所获利润最大?最大利润是多少?
(1)、求证:∠DHO=∠DCO.(2)、若OC=4,BD=6,求菱形ABCD的周长和面积.23. 某商店购进一批清洁剂,每瓶进价为20元,出于营销考虑,要求每瓶清洁剂的售价不低于20元且不高于28元,在销售过程中发现该清洁剂每周的销售量(瓶)与每瓶清洁剂的售价(元)之间满足一次函数关系:当销售单价为22元时,销售量为36瓶;当销售单价为24元时,销售量为32瓶.(1)、求出与的函数关系式,并写出的取值范围;(2)、设该商店每周销售这种清洁剂所获得的利润为元,将该清洁剂销售单价定为多少元时,才能使商店销售该清洁剂所获利润最大?最大利润是多少?

