2021年广东省梅州市五华县中考数学模拟训练试卷

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的倒数是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 下列四个图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 习近平总书记提出了五年“精准扶贫”的战略构想，意味着每年要减贫约11600000人，将数据11600000用科学记数法表示为（）

A、 $1.16 \times 10^{6}$ B、 $1.16 \times 10^{7}$ C、 $1.16 \times 10^{8}$ D、 $11.6 \times 10^{6}$

查看试题解析
4. 下面计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{5}$ B、 $3 a^{2} - a^{2} = 2$ C、 $4 a^{6} \div 2 a^{3} = 2 a^{2}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
5. 我市四月份某一周每天的最高气温（单位：℃）如下：20、21、22、22、24、25、27，则这组数据（最高气温）的众数与中位数分别是（）

A、22，24 B、24，24 C、22，22 D、25，22

查看试题解析
6. 如果一个多边形的每个外角都是 $60 °$ ，那么这个多边形是（）

A、五边形 B、六边形 C、七边形 D、八边形

查看试题解析
7. 如图，将△AOB绕着点O顺时针旋转，得到△COD，若∠AOB＝40°，∠BOC＝30°，则旋转角度是（）

A、10° B、30° C、40° D、70°

查看试题解析
8. 若方程x²﹣2x﹣k＝0没有实数根，则k的值可以为（）

A、1 B、0 C、﹣1 D、﹣2

查看试题解析
9. 如图，将函数y＝ $\frac{1}{2}$ （x﹣2）²+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（）

A、y＝ $\frac{1}{2}$ （x﹣2）²-2 B、y＝ $\frac{1}{2}$ （x﹣2）²+7 C、y＝ $\frac{1}{2}$ （x﹣2）²-5 D、y＝ $\frac{1}{2}$ （x﹣2）²+4

查看试题解析
10. 如图，在正方形 $A B C D$ 中，E，F分别是 $B C$ ， $C D$ 的中点， $A E$ 交BF于点H， $C G / / A E$ 交BF于点G，下列结论，① $s i n ∠ H B E = c o s ∠ H E B$ ；② $C G \cdot B F = B C \cdot C F$ ；③ $B H = F G$ ；④ $\frac{B C^{2}}{C F^{2}} = \frac{B G}{G F}$ .其中正确的是（）

A、①③④ B、①② C、②③ D、①②④

查看试题解析

二、填空题

11. 分解因式： $3 x^{2} + 6 x$ ．

查看试题解析
12. 如图，直线 $a / / b$ ， $∠ 1 = 130 °$ ，则 $∠ 2$ 的度数是.

查看试题解析
13. 已知 $∠ α = 65 ° 30'$ ，则 $∠ α$ 的余角大小是．

查看试题解析
14. 如图，四边形 $A B C D$ 是 $⊙ O$ 的内接四边形，对角线 $A C$ 是 $⊙ O$ 的直径， $A B = 2$ ， $∠ A D B = 45 °$ ，则 $⊙ O$ 的半径长为．

查看试题解析
15. 若点 $A (2 ， y_{1})$ 、 $B (3 ， y_{2})$ 都在反比例函数 $y = \frac{5}{x}$ 的图象上，则 $y_{1}$ $y_{2}$ （填“<”、“>”或“=”）．

查看试题解析
16. 定义新运算“ $a * b$ ”：对于任意实数 $a$ 、 $b$ ，都有 $a * b = (a + b) (a - b) - 1$ ，例 $4 * 3 = (4 + 3) (4 - 3) - 1 = 7 - 1 = 6$ ．若 $x * 2 = 4 x$ ，则x的值为．

查看试题解析
17. 如图，在四边形 $A B C D$ 中， $A B = C B ， A D = C D$ ．若 $∠ A B D = ∠ A C D = 30 ° ， A D = 1$ ，则 $△ A B C$ 的内切圆面积（结果保留 $π$ ）．

查看试题解析

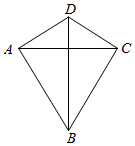
三、解答题

18. 解不等式组： ${\begin{array}{l} - 2 x < 4 \\ \frac{3 x - 1}{2} < 1 + x \end{array}$ ．

查看试题解析
19. 先化简，再求值： $(1 + \frac{3}{a - 1}) \div \frac{a^{2} + 4 a + 4}{2 a - 2}$ ，其中 $a = \sqrt{2} - 2$ ．

查看试题解析
20. 某校在创建书香校园活动中，为了解全校1600名学生年度课外阅读量，随机抽查了部分学生，并用得到的数据绘制了统计图，如图1和图2所示．请根据图中信息，解答下列问题：

(1)、补全学生年度课外阅读量条形统计图；

(2)、估算该校全体学生年度课外阅读量在8本以上（含8本）的学生总人数．

查看试题解析
21. 在Rt△ABC中，∠C=90°．

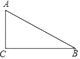(1)、求作：∠A的平分线AD，AD交BC于点D；（保留作图痕迹，不写作法）

(2)、若点D恰好在线段AB的垂直平分线上，求∠A的度数．

查看试题解析
22. 某种型号油电混合动力汽车，从A地到B地燃油行驶需纯燃油费用76元，从A地到B地用电行驶需纯用电费用26元，已知每行驶1千米，纯燃油费用比纯用电费用多0.5元．

(1)、求每行驶1千米纯用电的费用；

(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元，则至少需用电行驶多少千米？

查看试题解析
23. 如图，在平面直角坐标系xOy中，函数 $y= \frac{4}{x} (x > 0)$ 的图象与一次函数y=kx－k的图象的交点为A（m，2）.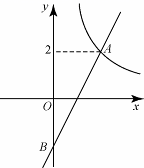

(1)、求一次函数的解析式；

(2)、设一次函数y=kx－k的图象与y轴交于点B，若P是x轴上一点，且满足△PAB的面积是4，直接写出点P的坐标.

查看试题解析
24. 如图，等边三角形 $△ A B E$ 和矩形 $A B C D$ 有共同的外接圆⊙O，且 $A B = 30$ ．

(1)、求证： $∠ C E D = 120 °$ ；

(2)、在劣弧 $\overset{⌢}{A B}$ 上有动点 $F$ ，连接 $D F$ 、 $C F$ 、 $B F$ ， $D F$ 分别交 $A E$ 、 $A B$ 于点 $M$ 、 $P$ ， $C F$ 交 $B E$ 于点 $N$ ．
①设 $△ M N F$ 与 $△ C D F$ 的周长分别为 $C_{1}$ 和 $C_{2}$ ，试判断 $C_{2} - C_{1}$ 的值是否发生变化，若不变则求出该值；若变化请说明理由；
②若 $P N = 5 \sqrt{3}$ ，求 $B F$ 的长．

查看试题解析
25. 如图①，抛物线 $y = - \frac{1}{4} x^{2} + b x + c$ 经讨点 $A (4 ， 3)$ 对称轴是直线 $x = 2$ .顶点为B．抛物线与y轴交于点C，连接 $A C$ ，过点 $A$ 作 $A D ⊥ x$ 轴于点D，点E是线段 $A C$ 上的动点（点E不与 $A$ 、C两点重合）.

(1)、求抛物线的函数解析式和顶点B的坐标；

(2)、若直线 $B E$ 将四边形 $A C O D$ 分成面积比为1：3的两个四边形，求点E的坐标；

(3)、如图②，连接DE，作矩形 $D E F G$ ，在点E的运动过程中，是否存在点 $G$ 落在y轴上的同时点F也恰好落在抛物线上？若存在，求出此时AE的长；若不存在，请说明理由.

查看试题解析