2021年广东省梅州市蕉岭县三校联合中考模拟数学考试卷
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
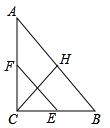
1. ﹣的绝对值是( )A、﹣2020 B、﹣ C、 D、20202. 已知一组数据为1,5,3,9,7,11.则这组数据的中位数是( )A、5 B、6 C、7 D、83. 在平面直角坐标系的第二象限内有一点 ,点 到 轴的距离为3,到 轴的距离为4,则点 的坐标是( )A、 B、 C、 D、4. 多边形的内角和不可能为( )A、180° B、540° C、1080° D、1200°5. 若式子 在实数范围内有意义,则 的取值范围是( )A、 且 B、 C、 且 D、6. 不等式组 的整数解共有( )A、1个 B、2个 C、3个 D、4个7. 如图,在 中, ,点H、E、F分别是边 、 、 的中点,若 ,则 的值为( )
 A、3 B、4 C、5 D、68. 在平面直角坐标系中,一次函数y=mx+b(m,b均为常数)与正比例函数y=nx(n为常数)的图象如图所示,则关于x的方程mx=nx﹣b的解为( )
A、3 B、4 C、5 D、68. 在平面直角坐标系中,一次函数y=mx+b(m,b均为常数)与正比例函数y=nx(n为常数)的图象如图所示,则关于x的方程mx=nx﹣b的解为( ) A、x=3 B、x=﹣3 C、x=1 D、x=﹣19. 如图,矩形ABCD中,点G , E分别在边BC , DC上,连接AG , EG , AE , 将△ABG和△ECG分别沿AG , EG折叠,使点B , C恰好落在AE上的同一点,记为点F . 若CE=3,CG=4,则DE的长度为( )
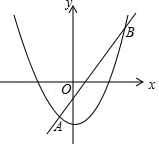
A、x=3 B、x=﹣3 C、x=1 D、x=﹣19. 如图,矩形ABCD中,点G , E分别在边BC , DC上,连接AG , EG , AE , 将△ABG和△ECG分别沿AG , EG折叠,使点B , C恰好落在AE上的同一点,记为点F . 若CE=3,CG=4,则DE的长度为( ) A、 B、 C、3 D、10. 已知抛物线y=a(x﹣3)2+过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切。正确的结论是( )
A、 B、 C、3 D、10. 已知抛物线y=a(x﹣3)2+过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切。正确的结论是( ) A、①③ B、①④ C、①③④ D、①②③④
A、①③ B、①④ C、①③④ D、①②③④二、填空题
-
11. 分解因式: =.12. 若7axb2与-a3by的和为单项式,则yx=.13. 已知 ,则 的值为 .14. 如图,抛物线y=ax2+c与直线y=﹣mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集是 .
 15. 如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.若AC=4,则EG2+FH2= .
15. 如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.若AC=4,则EG2+FH2= . 16. 如图,AB是⊙O的直径,C为圆周上一点,∠ACB的平分线CD交⊙O于D,连接AD,BD,若AD= , 则图中阴影部分的面积为 .
16. 如图,AB是⊙O的直径,C为圆周上一点,∠ACB的平分线CD交⊙O于D,连接AD,BD,若AD= , 则图中阴影部分的面积为 . 17. 如图,反比例函数 (x>0)的图象与直线 相交于点A,与直线y=kx(k≠0)相交于点B,若△OAB的面积为18,则k的值为.
17. 如图,反比例函数 (x>0)的图象与直线 相交于点A,与直线y=kx(k≠0)相交于点B,若△OAB的面积为18,则k的值为.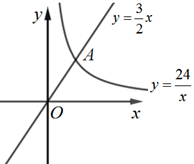
三、解答题
-
18. 先化简,再求值:(x﹣1﹣)÷ , 其中x=3.19. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
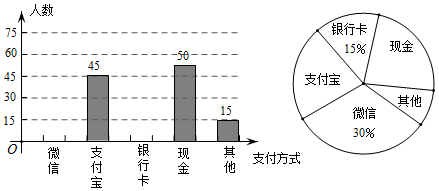 (1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是▲ ”;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.20. 如图,在△ABC中,AB=AC,∠BAC=80°,D是AC上一点,E是BC延长线上一点,连接BD,DE,若∠ABD=20°,BD=DE,求∠CDE的度数.
(1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是▲ ”;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.20. 如图,在△ABC中,AB=AC,∠BAC=80°,D是AC上一点,E是BC延长线上一点,连接BD,DE,若∠ABD=20°,BD=DE,求∠CDE的度数. 21. 关于x的一元二次方程x2﹣5x+k=0有实数根.(1)、求k的取值范围;(2)、如果k是符合条件的最大整数,且一元二次方程(m﹣1)x2+x+m﹣3=0与方程x2﹣5x+k=0有一个相同的根,求此时m的值.22. 如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,AD=BC,求证:四边形EFGH是菱形.
21. 关于x的一元二次方程x2﹣5x+k=0有实数根.(1)、求k的取值范围;(2)、如果k是符合条件的最大整数,且一元二次方程(m﹣1)x2+x+m﹣3=0与方程x2﹣5x+k=0有一个相同的根,求此时m的值.22. 如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,AD=BC,求证:四边形EFGH是菱形. 23. 某医院计划选购A、B两种防护服.已知A防护服每件价格是B防护服每件价格的1.5倍,用6000元单独购买A防护服比用5000元单独购买B防护服要少2件.(1)、A,B两种防护服每件价格各是多少元?(2)、如果该医院计划购买B防护服的件数比购买A防护服件数的3倍多80件,且用于购买A,B两种防护服的总经费不超过265000元,那么该医院最多可以购买多少件B防护服?
23. 某医院计划选购A、B两种防护服.已知A防护服每件价格是B防护服每件价格的1.5倍,用6000元单独购买A防护服比用5000元单独购买B防护服要少2件.(1)、A,B两种防护服每件价格各是多少元?(2)、如果该医院计划购买B防护服的件数比购买A防护服件数的3倍多80件,且用于购买A,B两种防护服的总经费不超过265000元,那么该医院最多可以购买多少件B防护服?