2021年广东省惠州市龙门县中考数学模拟试卷（三）

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣π的绝对值是（）

A、﹣π B、3.14 C、π D、 $\frac{1}{π}$

查看试题解析
2. 如图所示的几何体，从上面看得到的图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列说法正确的是（）

A、近似数0.21与0.210的精确度相同 B、小明的身高为161cm中的数是准确数 C、0.000109这个数用科学记数法可表示为1.09×10^﹣⁴ D、近似数1.3×10⁴精确到十分位

查看试题解析
5. 如图，AB∥CD，E为CD上一点，射线EF经过点A，EC=EA．若∠CAE=30°，则∠BAF=（）

A、30° B、40° C、50° D、60°

查看试题解析
6. 某同学从A地出发沿北偏东30°的方向步行5分钟到达B地，再由B地沿南偏西40°的方向步行到达C地，则∠ABC的大小为（）

A、10° B、20° C、35° D、70°

查看试题解析
7. 某校开设了冰球选修课，12名同学被分成甲、乙两组进行训练，他们的身高（单位：cm）如图所示：设两队队员身高的平均数依次为 $\bar{x_{甲}}$ ， $\bar{x_{乙}}$ ，方差依次为s_甲² ， s_乙² ，下列关系中完全正确的是（）

A、 $\bar{x_{甲}} = \bar{x_{乙}}$ ， s_甲²＜s_乙² B、 $\bar{x_{甲}} = \bar{x_{乙}}$ ， s_甲²＞s_乙² C、 $\bar{x_{甲}} < \bar{x_{乙}}$ ， s_甲²＜s_乙² D、 $\bar{x_{甲}} > \bar{x_{乙}}$ ， s_甲²＞s_乙²

查看试题解析
8. 如图，在长方形 $A B C D$ 中， $∠ A C B = 68 °$ ，依据尺规作图的痕迹，可求出 $∠ α$ 等于（）．

A、 $68 °$ B、 $56 °$ C、 $44 °$ D、 $34 °$

查看试题解析
9. 下列等式成立的是（）

A、 $\frac{1}{a} + \frac{2}{b} = \frac{3}{a + b}$ B、 $\frac{a b}{a b - b^{2}} = \frac{a}{a - b}$ C、 $\frac{2}{2 a + b} = \frac{1}{a + b}$ D、 $\frac{a}{- a + b} = - \frac{a}{a + b}$

查看试题解析
10. 如图，在平面直角坐标系中，正方形ABCD的顶点A的坐标为（ $\frac{\sqrt{5}}{5}$ ， 0），顶点D的坐标为（0， $\frac{2}{5} \sqrt{5}$ ），延长CB交x轴于点A₁ ，作正方形A₁B₁C₁C，延长C₁B₁交x轴于点A₂ ，作正方形A₂B₂C₂C₁ ， ……，按这样的规律进行下去，第2021个正方形的边长为（）

A、 ${(\frac{3}{2})}^{2019}$ B、 ${(\frac{3}{2})}^{2020}$ C、 ${(\frac{3}{2})}^{2021}$ D、 ${(\frac{3}{2})}^{2022}$

查看试题解析

二、填空题

11. 因式分解： $a^{3} - a b^{2}$ =.

查看试题解析
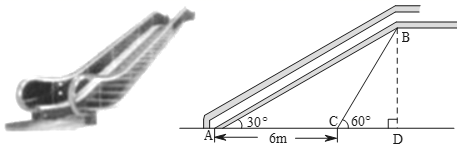
12. 若分式 $\frac{2 x - 3}{x + 1}$ 的值为0，则x的值为．

查看试题解析
13. 已知2x﹣3y﹣5＝0，则9y﹣6x＋16＝．

查看试题解析
14. 已经点P $(a + 2 ， a - 1)$ 在平面直角坐标系的第四象限，则 $a$ 的取值范围是.

查看试题解析
15. 如图是某商场自动扶梯的示意图，自动扶梯AB的倾斜角为30°，在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°，A、C之间的距离为6m，则自动扶梯的垂直高度BD=m．（结果保留根号）．

查看试题解析
16. 如图，四边形 $A B C D$ 和 $A E F G$ 都是正方形，点 $E ， G$ 分别在 $A B ， A D$ 上，点F在扇形 $A D B$ 的 $\overset{⌢}{D B}$ 上，已知正方形 $A B C D$ 的边长为1，则图中阴影部分的面积为．

查看试题解析
17. 如图，边长为2的正方形ABCD内接于⊙O，点E是 $\overset{⌢}{A B}$ 上一点（不与A、B重合），点F是 $\overset{⌢}{B C}$ 上一点，连接OE，OF，分别与AB，BC交于点G，B，且∠EOF＝90°．有下列结论：① $\overset{⌢}{A E}$ ＝ $\overset{⌢}{B F}$ ；②四边形OGBH的面积随着点E位置的变化而变化；③△GBH周长的最小值为2+ $\sqrt{2}$ ；④若BG＝1﹣ $\frac{\sqrt{3}}{3}$ ，则BG，GE， $\overset{⌢}{B E}$ 围成的面积是 $\frac{π}{12} + \frac{\sqrt{3}}{6}$ ，其中正确的是．（把所有正确结论的序号都填上）

查看试题解析

三、解答题

18. 先化简，再求值：（x+1）（x﹣1）+x（2﹣x），其中x= $\frac{1}{2}$ .

查看试题解析
19. 某校开展诵读“诗经、唐诗、宋词、四大名著”的活动，为了解学生对着四项诵读内容的喜爱程度，在全校学生中随机抽取部分学生进行问卷调查（在这四项诵读内容中，被调查的学生必须满足且只能选择一项）将收集的数据进行整理，并绘制了两幅不完整的统计图（如图）请跟进图中提供的信息，回答以下问题：

(1)、本次调查中，随机抽取的学生有人，其中喜爱诵读|宋词的有人．

(2)、补全条形统计图；

(3)、若该校有2000名学生，估计全校学生中约有多少人喜爱诵读|宋词？

查看试题解析
20. 关于x的方程 $2 x^{2} + (m + 2) x + m = 0$ ．

(1)、求证：方程总有两个实数根；

(2)、请你选择一个合适的m的值，使得方程的两个根都是整数，并求此时方程的根．

查看试题解析
21. 为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4800元．已知甲、乙两车单独运完此堆垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元．

(1)、求甲、乙两车单独运完此堆垃圾各需运多少趟？

(2)、若单独租用一台车，租用哪台车合算？

查看试题解析
22. 如图，在矩形ABCD中，AD＜2AB，点E是AD的中点，连接BE，将△ABE沿BE折叠后得到△GBE，延长BG交DC于点F，连接EF．

(1)、求证：△EGF≌△EDF；

(2)、若点F是CD的中点，BC＝8，求CD的长．

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与直线 $y = x - 1$ 交于点 $A (3 ， m)$

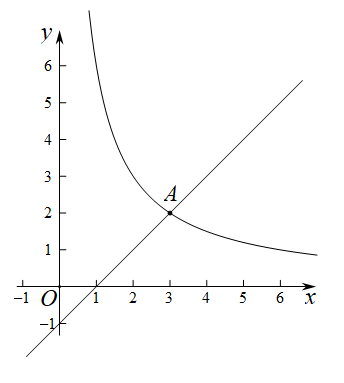(1)、求k的值；

(2)、已知点 $P (n ， 0) (n > 0)$ ，过点P作垂直于x轴的直线，交直线 $y = x - 1$ 于点B ，交函数 $y = \frac{k}{x} (x > 0)$ 于点C ．
①当 $n = 4$ 时，判断线段 $P C$ 与 $B C$ 的数量关系，并说明理由；

②若 $P C ⩽ B C$ ，结合图象，直接写出n的取值范围．

查看试题解析
24. 如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的圆O分别交AB，AC于点E，F，连接EF．

(1)、求证：BC是圆O的切线；

(2)、求证：AD²＝AF•AB；

(3)、若BE＝16，sinB $= \frac{5}{13}$ ，求AD的长．

查看试题解析
25. 如图，在平面直角坐标系中，已知抛物线y＝ax²＋bx＋8与x轴相交于A，B两点，与y轴相交于点C，OA＝4，OB＝2，点D是抛物线上一动点，且在y轴的左侧，连接AD，BC，AC，CD．

(1)、求抛物线的函数表达式；

(2)、已知直线y＝kx＋8与x轴相交于点M（点M与点B不重合），若以点M，C，O为顶点的△MCO与△BCO相似，求k的值；

(3)、连接OD，若△DAC的面积是△ABC的面积的 $\frac{1}{6}$ 时，求△CDO的面积．

查看试题解析