2021年广东省惠州市惠阳区大亚湾区中考数学二模试卷
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、-2 B、2 C、 D、2. 新型冠状病毒直径为 , 呈球形或椭圆形,具有多形性.如果米,那么新型冠状病毒的直径约为( )米A、 B、 C、 D、3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、等边三角形 B、平行四边形 C、正五边形 D、菱形4. 以下调查中,最适合采用全面调查的是( )A、检测长征运载火箭的零部件质量情况 B、了解全国中小学生课外阅读情况 C、调查某批次汽车的抗撞击能力 D、检测某城市的空气质量5. 不等式组的解集为( )A、无解 B、 C、 D、6. 实数 在数轴上的对应点的位置如图所示,则正确的结论是( )
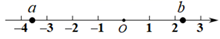 A、 B、 C、 D、7. 如图,三角板和直尺按如图所示的状态叠放着,若 , 则的大小为( )
A、 B、 C、 D、7. 如图,三角板和直尺按如图所示的状态叠放着,若 , 则的大小为( )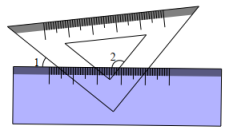 A、 B、 C、 D、8. 如图,已知圆心角∠AOB=110°,则圆周角∠ACB=( )
A、 B、 C、 D、8. 如图,已知圆心角∠AOB=110°,则圆周角∠ACB=( )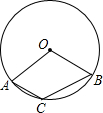 A、55° B、110° C、120° D、125°9. 如图,△ABC中,AB=AC,DE垂直平分AC,若△BCD的周长是14,BC=6,则AC的长是( )
A、55° B、110° C、120° D、125°9. 如图,△ABC中,AB=AC,DE垂直平分AC,若△BCD的周长是14,BC=6,则AC的长是( )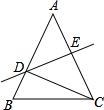 A、6 B、8 C、10 D、1410. 已知反比例函数 y=的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
A、6 B、8 C、10 D、1410. 已知反比例函数 y=的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )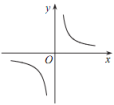 A、
A、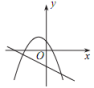 °
B、
°
B、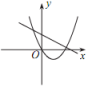 °
C、
°
C、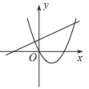 °
D、
°
D、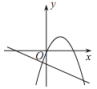
二、填空题
-
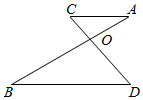
11. 分解因式:a2﹣2a+1= .12. 已知平面直角坐标系中的点P(a﹣3,2)在第二象限,则a的取值范围是13. 若 ,则 的值为 .14. 如图,AB,CD相交于O点,△AOC∽△BOD,OC:CD=1:3,AC=2,则BD的长为 .
 15. 已知代数式 , 那么代数式的值为 .16. 如图,将正方形绕着点逆时针旋转得到正方形 , 点的对应点落在正方形的对角线上,若 , 则的长为 .
15. 已知代数式 , 那么代数式的值为 .16. 如图,将正方形绕着点逆时针旋转得到正方形 , 点的对应点落在正方形的对角线上,若 , 则的长为 .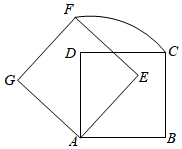 17. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过▱OABC的顶点C,则k= .
17. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过▱OABC的顶点C,则k= .
三、解答题
-
18. 计算: .19. 先化简,再求值: , 其中 , .20. 如图,在△ABC中,∠C=90°,∠ABC=60°.
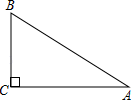 (1)、过点B作∠ABC的平分线交AC于点D(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);(2)、若AC=9,求点D到AB的距离.21. 某中学为了解学生对新闻、体育、娱乐,动画四类电视节目的喜爱情况,进行了统计调查,随机调查了某班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类),并将调查结果绘成如图不完整的统计图.
(1)、过点B作∠ABC的平分线交AC于点D(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);(2)、若AC=9,求点D到AB的距离.21. 某中学为了解学生对新闻、体育、娱乐,动画四类电视节目的喜爱情况,进行了统计调查,随机调查了某班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类),并将调查结果绘成如图不完整的统计图.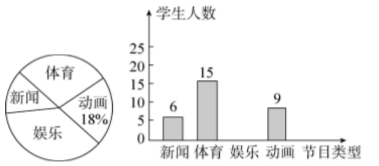
根据两图提供的信息,回答下列问题:
(1)、本次调查了多少人?(2)、请补全条形统计图;(3)、在全班同学中,甲 ,乙,丙,丁等同学最喜欢体育类节目,班主任打算从甲,乙,丙,丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同进选中甲,乙两同学的概率.22. 如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF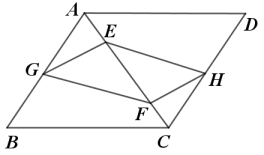 (1)、求证:四边形EGFH是平行四边形(2)、连接BD交AC于点O,若BD=10,AE+CF=EF,求EG的长23. 为迎接国庆节,某商店购进了一批成本为每件30元的纪念商品.经调查发现,该商品每天的销售量 (件 与销售单价 (元 满足一次函数关系,其图象如图所示.
(1)、求证:四边形EGFH是平行四边形(2)、连接BD交AC于点O,若BD=10,AE+CF=EF,求EG的长23. 为迎接国庆节,某商店购进了一批成本为每件30元的纪念商品.经调查发现,该商品每天的销售量 (件 与销售单价 (元 满足一次函数关系,其图象如图所示.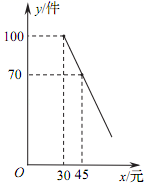 (1)、求该商品每天的销售量y与销售单价x的函数关系式;(2)、若商店按不低于成本价,且不高于60元的单价销售,则销售单价定为多少,才能使销售该商品每天获得的利润 (元 最大?最大利润是多少?24. 如图,已知AB是⊙O的直径,C是⊙O上一点(不与A、B重合),D为的 中点,过点D作弦DE⊥AB于F,P是BA延长线上一点,且∠PEA=∠B.
(1)、求该商品每天的销售量y与销售单价x的函数关系式;(2)、若商店按不低于成本价,且不高于60元的单价销售,则销售单价定为多少,才能使销售该商品每天获得的利润 (元 最大?最大利润是多少?24. 如图,已知AB是⊙O的直径,C是⊙O上一点(不与A、B重合),D为的 中点,过点D作弦DE⊥AB于F,P是BA延长线上一点,且∠PEA=∠B.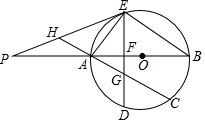 (1)、求证:PE是⊙O的切线;(2)、连接CA与DE相交于点G,CA的延长线交PE于H,求证:HE=HG;(3)、若tan∠P= ,试求 的值.25. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)、求证:PE是⊙O的切线;(2)、连接CA与DE相交于点G,CA的延长线交PE于H,求证:HE=HG;(3)、若tan∠P= ,试求 的值.25. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.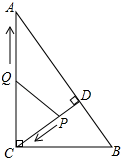 (1)、求线段CD的长;(2)、设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,则说明理由.(3)、是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,则说明理由.
(1)、求线段CD的长;(2)、设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,则说明理由.(3)、是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,则说明理由.