2021年广东省广州市花都区中考三模数学试卷

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2的绝对值是（）

A、 $\frac{1}{2}$ B、2 C、﹣2 D、0.5

查看试题解析
2. 在平面直角坐标系中，点 $(3 ， 2)$ 关于原点对称的点的坐标是（）

A、 $(2 ， 3)$ B、 $(- 3 ， 2)$ C、 $(- 3 ， - 2)$ D、 $(- 2 ， - 3)$

查看试题解析
3. 下列运算正确的是（）

A、2 $\sqrt{2} + 3 \sqrt{3} = 5 \sqrt{5}$ B、（ab）²＝ab² C、a³•a²＝a⁶ D、 $3 \sqrt{6} \div \sqrt{2} = 3 \sqrt{3}$

查看试题解析
4. 某校七年级共有1000名学生，为了解这些学生的视力情况，从中抽查了100名学生的视力，对所得数据进行整理．若视力在4.8～5.1这一组的频率为0.3，则可估计该校七年级学生视力在4.8～5.1范围内的人数约有（）

A、600人 B、300人 C、150人 D、30人

查看试题解析
5. 如图，AB为⊙O的切线，点A为切点，OB交⊙O于点C，点D在⊙O上，连接AD，CD，OA，若∠ADC＝25°，则∠ABO的度数为（）

A、35° B、40° C、50° D、55°

查看试题解析
6. 已知有1人患了某新型肺炎，经过两轮传染后共有256人患病，设每轮传染中平均一人传染x人，则可以列方程（）

A、1+2x＝256 B、1+x²＝256 C、（1+x）²＝256 D、1+x＝256

查看试题解析
7. 如图，函数 $y_{1} = m x$ 和 $y_{2} = x + 3$ 的图象相交于点 $A (- 1 ， 2)$ ，则关于x的不等式 $m x > x + 3$ 的解集是（）

A、 $x < - 1$ B、 $x > - 1$ C、 $x < - 2$ D、 $x > - 2$

查看试题解析
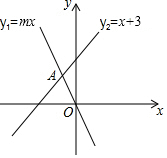8. 如图，在平行四边形ABCD中，E是AB边上一点，若AE：AB＝1：3，则S△AEF：S△ADC＝（）

A、1：12 B、1：9 C、1：6 D、1：3

查看试题解析
9. 若关于x的一元二次方程x²﹣2x﹣m＝0无实数根，则反比例函数 $y = \frac{m + 1}{x}$ 的图象可能经过点（）

A、（3，1） B、（0，3） C、（﹣3，﹣1） D、（﹣3，1）

查看试题解析
10. 如图1，在菱形ABCD中，AB＝6，∠BAD＝120°，点E是BC边上的一动点，点P是对角线BD上一动点，设PD的长度为x，PE与PC的长度和为y，图2是y关于x的函数图象，其中H（a，b）是图象上的最低点，则a+b的值为（）

A、 $7 \sqrt{3}$ B、 $6 \sqrt{3} + 3$ C、 $8 \sqrt{3}$ D、3 $\sqrt{3} +$ 6

查看试题解析

二、填空题

11. 已知：点M是线段 $A B$ 的中点，若线段 $A M = 3 cm$ ，则线段 $A B$ 的长度是 $cm$ ．

查看试题解析
12. 化简分式： $\frac{x - 1}{x + 1} + \frac{2}{1 + x}$ ＝．

查看试题解析
13. 如图，在3×3的正方形网格中，有三个小正方形已经涂成灰色，若再任意涂灰1个白色的小正方形（每个白色的小正方形被涂成灰轴对称图形的概率是图色的可能性相同，使新构成灰色部分的图形是轴对称图形的概率是．

查看试题解析
14. 已知关于x、y的方程组 ${\begin{array}{l} x + 2 y = 1 - a \\ 2 x + y = a + 8 \end{array}$ ，则代数式2x⁺y＝．

查看试题解析
15. 如图，圆锥的底面半径为3，侧面积为 $18 π$ ，设圆锥的母线与高的夹角为 $α$ ，则 $t a n α$ 的值是．

查看试题解析
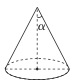16. 规定：经过三角形的一个顶点且将三角形的周长分成相等的两部分的直线叫做该角形的“等周线”，“等周线”被这个三角形截得的线段叫做该三角形的“等周径”．例如等腰三角形底边上的中线即为它的“等周径”Rt△ABC中，∠C＝90°，AC＝4，BC＝3，若直线 $l$ 为△ABC的“等周线”，则△ABC的所有“等周径”长为．

查看试题解析

三、解答题

17. 解不等式：5x﹣1＞3（x+5）．

查看试题解析
18. 如图，E为BC上一点，AC∥BD，AC＝BE，∠ABC＝∠D．求证：AB＝ED．

查看试题解析
19. 已知T＝（a+1）（a﹣1）﹣a（a+2）．

(1)、化简T；

(2)、若点M（2，a）在一次函数y＝x+1的图象上，求T的值．

查看试题解析
20. 如图，在高度为10米的建筑平台CD的顶部C处，测得大楼AB的顶部A的仰角α＝45°，测得大楼AB的底部B的俯角β＝30°，求大楼AB的高度（精确到0.1米，参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）．

查看试题解析
21. 某医药公司计划招聘一名科研人员，组织了一场“云招聘”，甲、乙两名应聘者的成绩如下表所示（单位：分）．
应聘者
专业知识
创新能力
语言表达
甲
96
92
85
乙
93
88
95

(1)、根据实际需要，该公司计划将专业知识、创新能力、语言表达三项按3：5：2的比例计算最后成绩，请计算甲、乙两人的最后成绩．

(2)、为了更全面地了解甲、乙两名应聘者的综合素质，公司决定安排一场加试．加试设置三项综合性任务（依次记为A、B、C），要求甲、乙二人分别从这三项任务中随机选择一项完成并提交报告．求甲、乙二人所选任务不相同的概率．

查看试题解析
22. 如图，⊙O是△ABC的外接圆，BC是⊙O的直径．

(1)、尺规作图：在优弧ACB上作点D，使得AD＝AB；作射线BD，与线段AC的延长线交于点E．（保留作图痕迹，不要求写作法）

(2)、在（1）的条件下：
①求证：△ABC∽△AEB；
②若AC＝1，CE＝3，求⊙O的半径．

查看试题解析
23. 如图，矩形OABC的顶点B的坐标为（4，2），双曲线 $y = \frac{k}{x}$ （x＞0）与矩形的对角线OB交于点D，与AB、BC分别交于点E、F，且点F是BC的中点．

(1)、求点E的坐标；

(2)、连接AD，求△ABD的面积．

查看试题解析
24. △ABC为等腰三角形，AB＝AC，点D为△ABC所在平面内一点．

(1)、若∠BAC＝120°，
①如图1，当点D在BC边上，BD＝AD，求证：DC＝2BD；
②如图2，当点D在△ABC外，∠ADB＝120°，AD＝2，BD＝4，连接CD，求CD的长；

(2)、如图3，当点D在△ABC外，且∠ADB＝90°，以AD为腰作等腰三角形△ADE，∠DAE＝∠BAC，AD＝AE，直线DE交BC于点F，求证：点F是BC中点．

查看试题解析
25. 如图，抛物线y＝ax²+bx+2经过A（﹣1，0），B（4，0）两点，与y轴交于点C．

(1)、求该抛物线的解析式；

(2)、在y轴上是否存在点P使得∠OBP+∠OBC＝45°，若存在，求出点P的坐标，若不存在，请说明理由；

(3)、点M是BC为直径的圆上的动点，将点M绕原点O顺时针旋转90°得点N，连接NA，求NA的取值范围．

查看试题解析

应聘者	专业知识	创新能力	语言表达
甲	96	92	85
乙	93	88	95