2021年广东省佛山市禅城区中考数学二模试卷
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 下列四个数中,最小的数是( )A、1 B、﹣2 C、 D、0.012. 如图所示图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2020年6月23日,北斗卫星系统最后一颗全球组网卫星发射成功.北斗卫星距地球大约为35800km,35800用科学记数法可表示为( )A、3.58×103 B、3.58×104 C、3.58×105 D、3.58×1064. 化简的结果是( )A、2 B、6 C、4 D、25. 把一张宽度相等的纸条按如图所示的方式折叠,则∠1 的度数等于( )
3. 2020年6月23日,北斗卫星系统最后一颗全球组网卫星发射成功.北斗卫星距地球大约为35800km,35800用科学记数法可表示为( )A、3.58×103 B、3.58×104 C、3.58×105 D、3.58×1064. 化简的结果是( )A、2 B、6 C、4 D、25. 把一张宽度相等的纸条按如图所示的方式折叠,则∠1 的度数等于( )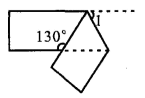 A、65° B、55° C、45° D、50°6. 八年级(1)班甲、乙、丙、丁四名同学几次数学测试成绩的平均数(分)及方差如表,老师想从中选派一名成绩较好且状态稳定的同学参加省初中生数学竞赛,那么应选( )
A、65° B、55° C、45° D、50°6. 八年级(1)班甲、乙、丙、丁四名同学几次数学测试成绩的平均数(分)及方差如表,老师想从中选派一名成绩较好且状态稳定的同学参加省初中生数学竞赛,那么应选( )甲
乙
丙
丁
平均数(分)
95
97
95
97
方差
0.5
0.5
0.2
0.2
A、甲 B、乙 C、丙 D、丁7. 如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( ) A、2 B、4 C、 D、8. 从甲、乙、丙、丁四人中用抽签的方式,随机选取两人打扫卫生,那么选中的两人是甲和乙的概率为( )A、 B、 C、 D、9. 已知方程x2+6x﹣m=0的一个根为﹣2.则方程的另外一根为( )A、﹣8 B、8 C、﹣4 D、410. 如图,A、B分别为反比例函数(x<0),y=(x>0)图象上的点,且OA⊥OB,则tan∠ABO的值为( )
A、2 B、4 C、 D、8. 从甲、乙、丙、丁四人中用抽签的方式,随机选取两人打扫卫生,那么选中的两人是甲和乙的概率为( )A、 B、 C、 D、9. 已知方程x2+6x﹣m=0的一个根为﹣2.则方程的另外一根为( )A、﹣8 B、8 C、﹣4 D、410. 如图,A、B分别为反比例函数(x<0),y=(x>0)图象上的点,且OA⊥OB,则tan∠ABO的值为( )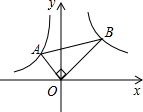 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
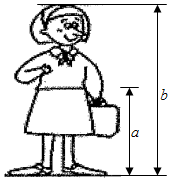
11. 若a、b互为相反数,则a+(b﹣2)的值为.12. 若amb3与﹣7abn是同类项,则m+n= .13. 分解因式: =.14. 正多边形的一个内角等于144°,则这个多边形的边数是 .15. 古希腊时期,人们认为最美人体的头顶至腰部的长度与腰部至足底的长度之比是黄金分割比例.在设计人体雕像时,雕像(如图所示)的腰部以下长为a,身高b的,如果我们选择最美设计方案,当b为2米时,则a约为米.(≈2.236,精确到0.01米)
 16. 如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是 .
16. 如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是 .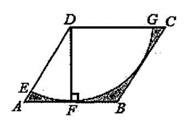 17. 如图,抛物线y=ax2+bx+c(a≠0)与轴交于点A(﹣2,0)、B(1,0),抛物线对称轴x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,小明根据图象写出下列结论:①a﹣b=0:②当﹣2<x<1时,y>0;③四边形ACBD是菱形;④9a﹣3b+c>0;其中正确的是(填序号).
17. 如图,抛物线y=ax2+bx+c(a≠0)与轴交于点A(﹣2,0)、B(1,0),抛物线对称轴x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,小明根据图象写出下列结论:①a﹣b=0:②当﹣2<x<1时,y>0;③四边形ACBD是菱形;④9a﹣3b+c>0;其中正确的是(填序号).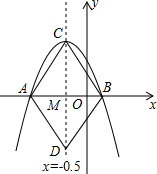
三、解答题
-
18. 计算: .19. 先化简,再求代数式的值,且为满足的整数.20. 如图1,在△ABC中,D是AB边上的一点,小明用尺规作图,做法如下:如图,①以B为圆心,任意长为半径作弧,交BA于F、交BC于G;②以D为圆心,BF为半径作弧,交DA于M;③以M为圆心,FG为半径作弧,两弧相交于N;④过点D作射线DN交AC于点E.根据上述材料,解答下列问题:
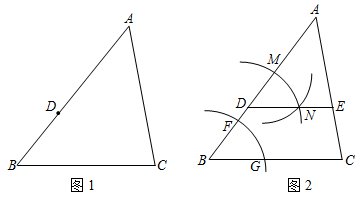 (1)、由作图过程可以推导出DEBC,依据的定理是;(2)、若AD=2,DB=1,DE=1.5,求BC的长度.21. 某校760名学生参加植树活动,要求每人植树的范围是2≤x≤5棵,活动结束后随机抽查了若名学生每人的植树量,并分为四种类型,A:2棵;B:3棵;C:4棵;D:5棵,将各类的人数绘制成扇形统计图(如图2)和条形统计图(如图1).回答下列问题:
(1)、由作图过程可以推导出DEBC,依据的定理是;(2)、若AD=2,DB=1,DE=1.5,求BC的长度.21. 某校760名学生参加植树活动,要求每人植树的范围是2≤x≤5棵,活动结束后随机抽查了若名学生每人的植树量,并分为四种类型,A:2棵;B:3棵;C:4棵;D:5棵,将各类的人数绘制成扇形统计图(如图2)和条形统计图(如图1).回答下列问题: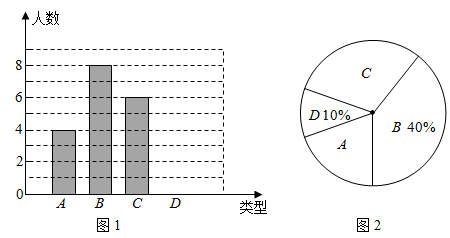 (1)、补全条形统计图;(2)、被调查学生每人植树量的众数、中位数分别是多少?(3)、估计该校全体学生在这次植树活动中共植树多少棵?22. 4月23日为“世界读书日”.每年的这一天,各地都会举办各种宣传活动.我市某书店为迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
(1)、补全条形统计图;(2)、被调查学生每人植树量的众数、中位数分别是多少?(3)、估计该校全体学生在这次植树活动中共植树多少棵?22. 4月23日为“世界读书日”.每年的这一天,各地都会举办各种宣传活动.我市某书店为迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:“读书节”活动计划书
图书类别
A类
B类
进价
18元/本
12元/本
备注
(1)用不超过16800元购进AB两类图书共1000本;
(2)A类图书不少于600本;
(1)、陈经理查看计划书时发现:A类图书的销售价是B类图书销售价的1.5倍,若顾客同样用54元购买图书,能购买A类图书数量比B类图书的数量少1本,求A、B两类图书的销售价;(2)、为了扩大影响,陈经理调整了销售方案:A类图书每本按原销售价降低2元销售,B类图书价格不变,那么该书店应如何进货才能获得最大利润?23. 如图,一次函数y=k1x+b与反比例函数y=图象交于点B(﹣1,6)、点A,且点A的纵坐标为3. (1)、填空:k1= , b=;k2=;(2)、结合图形,直接写出k1x+b>时x的取值范围;(3)、在梯形ODCA中,ACOD,且下底DO在x轴上,CD⊥x轴于点D,CD和反比例函数的图象交于点M,当梯形ODCA的面积为12时,求此时点M坐标.24. 如图1,AB是⊙O的直径,C是⊙O上一点,过点B作⊙O的切线,与AC的延长线相交于点D,E是BD的中点,分别延长AB、CE相交于点P;
(1)、填空:k1= , b=;k2=;(2)、结合图形,直接写出k1x+b>时x的取值范围;(3)、在梯形ODCA中,ACOD,且下底DO在x轴上,CD⊥x轴于点D,CD和反比例函数的图象交于点M,当梯形ODCA的面积为12时,求此时点M坐标.24. 如图1,AB是⊙O的直径,C是⊙O上一点,过点B作⊙O的切线,与AC的延长线相交于点D,E是BD的中点,分别延长AB、CE相交于点P;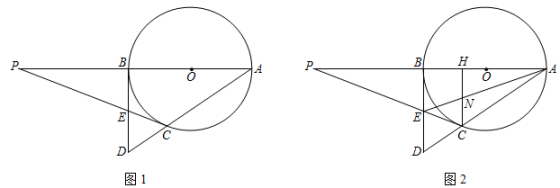 (1)、求证:PC是⊙O的切线;(2)、如图2,若CH⊥AB于H,连接AE与交CH于N,求证:N是HC的中点;(3)、在(2)的条件下,若BE=EN,且BH=2,求⊙O的半径.25. 如图1,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,直线BC的解析式为y=x﹣4;线段OC的垂直平分线交抛物线于点M、N,点M、N横坐标分别为x1、x2且满足x1+x2=3.
(1)、求证:PC是⊙O的切线;(2)、如图2,若CH⊥AB于H,连接AE与交CH于N,求证:N是HC的中点;(3)、在(2)的条件下,若BE=EN,且BH=2,求⊙O的半径.25. 如图1,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,直线BC的解析式为y=x﹣4;线段OC的垂直平分线交抛物线于点M、N,点M、N横坐标分别为x1、x2且满足x1+x2=3.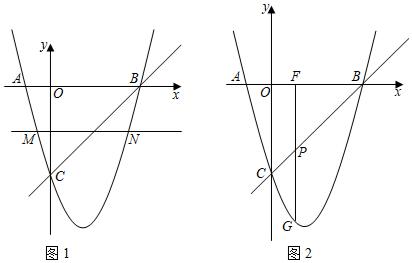 (1)、求抛物线的解析式;(2)、设点Q是直线MN上一动点,当点Q在什么位置上时,△QOB的周长最小?求出此时点Q的坐标及△QOB周长的最小值;(3)、如图2,P线段CB上的一点,过点P作直线PF⊥x轴于F,交抛物线于G,且PF=PG;点H是直线BC上一个动点,点Q是坐标平面内一点,以点H,Q,P,F为顶点的四边形是菱形,求所有满足条件的Q点坐标(写出其中一个点的坐标的详细求解过程,其余的点的坐标直接写出即可).
(1)、求抛物线的解析式;(2)、设点Q是直线MN上一动点,当点Q在什么位置上时,△QOB的周长最小?求出此时点Q的坐标及△QOB周长的最小值;(3)、如图2,P线段CB上的一点,过点P作直线PF⊥x轴于F,交抛物线于G,且PF=PG;点H是直线BC上一个动点,点Q是坐标平面内一点,以点H,Q,P,F为顶点的四边形是菱形,求所有满足条件的Q点坐标(写出其中一个点的坐标的详细求解过程,其余的点的坐标直接写出即可).