2021-2022学年初中数学北师大版八年级下册期末测试卷
试卷更新日期:2022-03-07 类型:期末考试
一、单选题
-
1. 下面四个图形中,既是轴对称图形也是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若式子有意义,则实数m的取值范围是( )A、且 B、且 C、 D、3. 多边形的内角和不可能为( )A、180° B、540° C、1080° D、1200°4. 如图,CD是等腰三角形 △ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,则 △ BCE的面积是( )
2. 若式子有意义,则实数m的取值范围是( )A、且 B、且 C、 D、3. 多边形的内角和不可能为( )A、180° B、540° C、1080° D、1200°4. 如图,CD是等腰三角形 △ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,则 △ BCE的面积是( ) A、4 B、6 C、8 D、125. 已知等边△ABC的边长为12, D是边AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )A、3 B、4 C、8 D、96. 当x分别取2020、2018、2016、…、4、2、0、、、…、、、时,计算分式的值,再将所得的结果全部相加,则其和等于( ).A、-1 B、1 C、0 D、20207. 若实数 既使得关于 的不等式组 有解,又使得关于 的分式方程 有整数解,则满足条件的所有整数 的和为( )A、4 B、2 C、0 D、-28. 在△ABC中,∠BAC=90°,点D在边BC上,AD=AB ( )
A、4 B、6 C、8 D、125. 已知等边△ABC的边长为12, D是边AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )A、3 B、4 C、8 D、96. 当x分别取2020、2018、2016、…、4、2、0、、、…、、、时,计算分式的值,再将所得的结果全部相加,则其和等于( ).A、-1 B、1 C、0 D、20207. 若实数 既使得关于 的不等式组 有解,又使得关于 的分式方程 有整数解,则满足条件的所有整数 的和为( )A、4 B、2 C、0 D、-28. 在△ABC中,∠BAC=90°,点D在边BC上,AD=AB ( ) A、若AC=2AB,则∠C=30° B、若AC=2AB,则3BD=2CD C、若∠B=2∠C,则AC=2AB D、若∠B=2∠C,则S△ABD=2△ACD
A、若AC=2AB,则∠C=30° B、若AC=2AB,则3BD=2CD C、若∠B=2∠C,则AC=2AB D、若∠B=2∠C,则S△ABD=2△ACD二、填空题
-
9. 分解因式:3m2﹣48= .10. 如图,平行四边形ABCD中,点O是对角线AC的中点,点E在边AB上,连接DE , 取DE的中点F , 连接EO并延长交CD于点G . 若BE=3CG , OF=2,则线段AE的长是 .
 11. 如图,D、E分别是AC和AB上的点,AD=DC=8,DE=6,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为.
11. 如图,D、E分别是AC和AB上的点,AD=DC=8,DE=6,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为.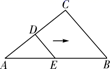 12. 若 ,则分式 的值为 .13. 若关于x的方程﹣5=无解,则m的值为 .14. 函数的图象如图,不等式的解集为.
12. 若 ,则分式 的值为 .13. 若关于x的方程﹣5=无解,则m的值为 .14. 函数的图象如图,不等式的解集为.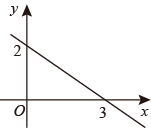 15. 在 中, , , ,点D、E分别在边 、 上,且 , ,将 绕点B旋转至 ,点D、E分别对应点 、 ,当 、 、 三点共线时, 的长为 .16. 我国过年历史悠久,在传承发展中己形成了一些较为固定的习俗,有许多还相传至今,如买年货、扫尘、贴对联、吃年夜饭、守岁、拜岁、拜年、舞龙舞狮、拜神祭祖、祈福攘灾、游神、押舟、庙会、游锣鼓、游标旗、上灯酒、赏花灯等.某商店新进一批“福”字贴画和数对灯笼(灯笼一对为2件),共超过250件但不超过300件,灯笼的对数正好是“福”字贴画数量的 ,每张“福”字贴画进价是4元,每对灯笼的进价是50元(灯笼成对出售),商店将“福”字贴画以高出进价的 售出,将灯笼每对按高出进价的40%售出,最后留下了35件物品未卖出,并把这批物品免费送给了自己的亲戚朋友,最后商店经过计算总利润率为20%,则最初购进灯笼对.
15. 在 中, , , ,点D、E分别在边 、 上,且 , ,将 绕点B旋转至 ,点D、E分别对应点 、 ,当 、 、 三点共线时, 的长为 .16. 我国过年历史悠久,在传承发展中己形成了一些较为固定的习俗,有许多还相传至今,如买年货、扫尘、贴对联、吃年夜饭、守岁、拜岁、拜年、舞龙舞狮、拜神祭祖、祈福攘灾、游神、押舟、庙会、游锣鼓、游标旗、上灯酒、赏花灯等.某商店新进一批“福”字贴画和数对灯笼(灯笼一对为2件),共超过250件但不超过300件,灯笼的对数正好是“福”字贴画数量的 ,每张“福”字贴画进价是4元,每对灯笼的进价是50元(灯笼成对出售),商店将“福”字贴画以高出进价的 售出,将灯笼每对按高出进价的40%售出,最后留下了35件物品未卖出,并把这批物品免费送给了自己的亲戚朋友,最后商店经过计算总利润率为20%,则最初购进灯笼对.三、计算题
-
17.(1)、计算:(2)、解不等式组:
四、解答题
-
18. 先化简,再求值: ,其中 ,且x是整数.19. 如图所示,在ABCD中,分别以AB,CD为边向外作等边△ABE和等边△CDF,连结BD,EF。求证:EF与BD互相平分。

五、综合题
-
20. 新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控.某呼吸机厂接到生产600台呼吸机的任务,以每天比原来多生产50台呼吸机的速度进行生产,结果所用时间与原来生产450台呼吸机所用时间相同.(1)、求该厂现在每天生产多少台呼吸机?(2)、完成这批任务后,该厂又接到在10天内至少生产2400台呼吸机的任务,问该厂每天还应该至少比现在多生产多少台呼吸机才能完成任务?21. 如图,AC是平行四边形ABCD的对角线.
 (1)、尺规作图:作线段AC的垂直平分线l(不写作法,保留作图痕迹);(2)、直线l分别交AB,AC,CD于点E,F,G.猜想DG与BE存在的数量关系,并证明你猜想的结论.22. 阅读材料:
(1)、尺规作图:作线段AC的垂直平分线l(不写作法,保留作图痕迹);(2)、直线l分别交AB,AC,CD于点E,F,G.猜想DG与BE存在的数量关系,并证明你猜想的结论.22. 阅读材料:《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂,从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
例如:已知 ,求 的值.
解:原式 .
问题解决:
(1)、已知 .①代数式 的值为 ▲ ;
②求证: .
(2)、若x满足 ,求 的值.23. 如图
 (1)、如图1,在▱ABCD中,AE平分∠BAD交CD边于点E,已知AB=5cm,AD=3cm,则EC等于cm。(2)、如图2,在▱ABCD中,若AE,BE分别是∠DAB,∠CBA的平分线,点E在DC边上,且AB=4,则ABCD的周长为。(3)、如图3,已知四边形ABCD是平行四边形,AD=BC,若AF,BE分别是∠DAB,∠CBA的平分线。求证:DF=EC(4)、在(3)的条件下,如果AD=3,AB=5,则EF的长为。24.
(1)、如图1,在▱ABCD中,AE平分∠BAD交CD边于点E,已知AB=5cm,AD=3cm,则EC等于cm。(2)、如图2,在▱ABCD中,若AE,BE分别是∠DAB,∠CBA的平分线,点E在DC边上,且AB=4,则ABCD的周长为。(3)、如图3,已知四边形ABCD是平行四边形,AD=BC,若AF,BE分别是∠DAB,∠CBA的平分线。求证:DF=EC(4)、在(3)的条件下,如果AD=3,AB=5,则EF的长为。24. (1)、阅读理解:问题:如图1,在四边形 中,对角线 平分 , .求证: .
(1)、阅读理解:问题:如图1,在四边形 中,对角线 平分 , .求证: .思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在 上截取 ,连接 ,得到全等三角形,进而解决问题;
方法2:延长 到点N,使得 ,连接 ,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种 , 添加辅助线并完成证明.
(2)、问题解决:如图2,在(1)的条件下,连接 ,当 时,探究线段 , , 之间的数量关系,并说明理由;(3)、问题拓展:如图3,在四边形 中, , ,过点D作 ,垂足为点E,请直接写出线段 、 、 之间的数量关系.
-