2021-2022学年初中数学北师大版八年级下册期中考试卷

试卷更新日期：2022-03-06 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，可以看作是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，把△ABC绕顶点C按顺时针方向旋转得到△A′B′C′，当A′B′⊥AC，∠A＝50°，∠A′CB＝115°时，∠B′CA的度数为（）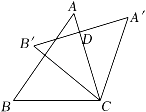

A、30° B、35° C、40° D、45°

查看试题解析
3. 下列说法正确的是（）

A、若a＜b，则3a＜2b B、若a＞b，则ac²＞bc² C、若﹣2a＞2b，则a＜b D、若ac²＜bc² ，则a＜b

查看试题解析
4. 如图，某研究性学习小组为测量学校A与河对岸村庄B之间的距离，在学校附近选一点C，利用测量仪器测得∠A=60°，∠C=90°，AC=2km．据此，可求得学校与村庄之间的距离AB等于（）

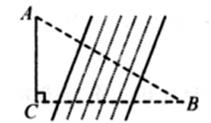A、2km B、3km C、2 $\sqrt{3}$ km D、4km

查看试题解析
5. 到三角形三边距离相等的点是（　　）

A、三边垂直平分线的交点 B、三条高所在直线的交点 C、三条角平分线的交点 D、三条中线的交点

查看试题解析
6. 如图，在△ABC中，AB＝AC，AB的垂直平分线交AB于点E，交BC于点F，连接AF，若∠FAC＝ $\frac{21}{5}$ ∠B，则∠FAB的度数为（）

A、25° B、30° C、35° D、50°

查看试题解析
7. 已知关于 $x$ 的不等式组 ${\begin{array}{l} x > m \\ x + 1 \leq 3 m \end{array}$ 有且只有两个整数解，则 $m$ 的取值范围是（）

A、 $1 < m \leq \frac{4}{3}$ B、 $1 \leq m < \frac{4}{3}$ C、 $\frac{4}{3} < m \leq \frac{5}{3}$ D、 $\frac{4}{3} \leq m < \frac{5}{3}$

查看试题解析
8. 如图，在 $△ A B C$ 中， $A C = B C$ ， $∠ B = 30 °$ ，D为 $A B$ 的中点，P为 $C D$ 上一点，E为 $B C$ 延长线上一点，且 $P A = P E .$ 有下列结论：① $∠ P A D + ∠ P E C = 30 °$ ；② $△ P A E$ 为等边三角形；③ $P D = C E - C P$ ；④ $S_{四边形 A E C P} = S_{△ A B C} .$ 其中正确的结论是（）

A、①②③④ B、①② C、①②④ D、③④

查看试题解析

二、填空题

9. 将一次函数y=5x-1的图象向上平移3个单位，所得直线不经过第象限．

查看试题解析
10. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 40 °$ ．将 $△ A B C$ 绕点B逆时针旋转得到 $△ A' B C'$ ，使点C的对应点 $C'$ 恰好落在边AB上，则 $∠ B A' A$ 的度数是．

查看试题解析
11. 等腰三角形ABC中，AB=AC，∠A=4∠B，则∠C=。

查看试题解析
12. 在平面直角坐标系中，一次函数 $y_{1} = k x$ （ $k$ 是常数， $k \neq 0$ ）与 $y_{2} = m x + n$ （m、n是常数， $m \neq 0$ ）的图象如图所示，则关于x的不等式 $k x > m x + n$ 的解集为.

查看试题解析
13. 如图，等腰△BAC中，∠BAC＝120°，BC＝6，P为射线BA上的动点，M为BC上一动点，则PM+CP的最小值为．

查看试题解析
14. 定义新运算：对于任意实数a，b都有：a⊕b＝a（a﹣b）+1.如：2⊕5＝2×（2﹣5）+1＝2×（﹣3）+1＝﹣5，那么不等式﹣3⊕x＜15的解为 .

查看试题解析
15. 如图，在平面直角坐标系中，将 $△ A B O$ 沿x轴向右滚动到 $△ A B_{1} C_{1}$ 的位置，再到 $△ A_{1} B_{1} C_{2}$ 的位置…依次进行下去，若已知点 $A (3 ， 0) ， B (0 ， 4)$ ，则点 $A_{49}$ 的坐标为.

查看试题解析
16. 如图，在△ABC中，AC＝BC＝13，AB＝24，D是AB边上的一个动点，点E与点A关于直线CD对称，当△ADE为直角三角形时，则AD的长为.

查看试题解析

三、解答题

17. 如图，在 $△ A B C$ 中， $B C = 10$ ， $A B$ 的垂直平分线分别交 $A B$ 、 $B C$ 于点D、E， $A C$ 的垂直平分线分别交 $A C$ 、 $B C$ 于点F、G.求 $△ A E G$ 的周长.

查看试题解析
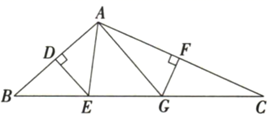18. 解不等式组： ${\begin{array}{l} 6 (\frac{2}{3} x - 2) < x - 3 \\ \frac{1 - x}{2} - 2 ⩽ x \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
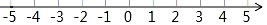19. 如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）．

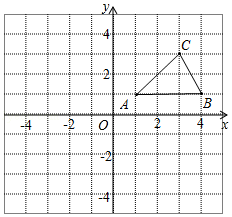(1)、将△ABC向下平移5个单位后得到△A₁B₁C₁ ，请画出△A₁B₁C₁；

(2)、将△ABC绕原点O逆时针旋转90°后得到△A₂B₂C₂ ，请画出△A₂B₂C₂；

(3)、判断以O，A₁ ， B为顶点的三角形的形状．（无须说明理由）

查看试题解析
20. 某店主购进 $A$ ， $B$ 两种礼盒.已知 $A$ ， $B$ 两种礼盒的单价比为2∶3，单价和为10元.该店主进 $B$ 种礼盒的数量是 $A$ 种礼盒数量的2倍少1个，且这两种礼盒花费不超过398元，则 $A$ 种礼盒最多购买多少个？

查看试题解析
21. 如图，在 $△ A B C$ 中，D为 $B C$ 的中点， $D E ⊥ A B$ ， $D F ⊥ A C$ ，垂足分别为E，F，且 $B E = C F$ ， $∠ B D E = 30^{o}$ ，求证： $△ A B C$ 是等边三角形.

查看试题解析
22. 如图，在 $△ A B C$ 中， $D$ 是 $B C$ 的中点， $D E ⊥ A B$ ， $D F ⊥ A C$ ，垂足分别是 $E$ ， $F$ ．
（Ⅰ）若 $B E = C F$ ，求证： $A D$ 是 $△ A B C$ 的角平分线；
（Ⅱ）若 $A D$ 是 $△ A B C$ 的角平分线，求证： $B E = C F$ ．

查看试题解析

四、综合题

23. 为响应国家“篮球进校园”的号召，某校购买了50个A型篮球和20个B型篮球共花费5000元，已知购买一个B型篮球比购买一个A型篮球多花40元.

(1)、求购买一个A型篮球和一个B型篮球各需多少元；

(2)、通过全校师生的共同努力，今年该校被评为“篮球特色学校”，学校计划用不超过4600元的经费再次购买A型篮球和B型篮球共50个，其中B型篮球的数量不少于A型篮球数量的 $\frac{1}{4}$ ，求A型篮球数量的取值范围；

(3)、报价如下表：
型号
购买数量少于30个
购买数量不少于30个
A型
原价购买
打九折
B型
原价购买
打八折
在（2）的条件下，设购买总花费为w元，问如何购买使得总花费w最少？请说明理由.

查看试题解析
24. 如图， $△ A B C$ 和 $△ A D E$ 中， $A B = A D = 6 ， B C = D E ， ∠ B = ∠ D = 30 °$ ， $A D$ 与 $B C$ 交于点P（不与点B，C重合），点B，E在 $A D$ 异侧， $∠ P A C$ 、 $∠ A C P$ 的平分线相交于点I.

(1)、当 $A D ⊥ B C$ 时，求 $P D$ 的长；

(2)、求证： $∠ B A D = ∠ C A E$ ；

(3)、当 $A B ⊥ A C$ 时， $∠ A I C$ 的取值范围为 $m ° < ∠ A I C < n °$ ，求m，n的值.

查看试题解析

型号	购买数量少于30个	购买数量不少于30个
A型	原价购买	打九折
B型	原价购买	打八折