初中数学北师大版八年级下册第六章 平行四边形 全章测试
试卷更新日期:2022-03-05 类型:单元试卷
一、单选题
-
1. 下列多边形中,内角和与外角和相等的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在四边形ABCD中,O是对角线交点,下列条件中,不能判定四边形ABCD是平行四边形的是( )A、AD∥BC,AD=BC B、AB=DC,AD=BC C、AB∥DC,AD=BC D、OA=OC,OD=OB3. 一个多边形截去一个角后,形成的另一个多边形的内角和为720°,那么原多边形的边数为( )A、5 B、5或6 C、5或7 D、5或6或74. 如图所示 , □ABCD的面积是12,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( )
2. 在四边形ABCD中,O是对角线交点,下列条件中,不能判定四边形ABCD是平行四边形的是( )A、AD∥BC,AD=BC B、AB=DC,AD=BC C、AB∥DC,AD=BC D、OA=OC,OD=OB3. 一个多边形截去一个角后,形成的另一个多边形的内角和为720°,那么原多边形的边数为( )A、5 B、5或6 C、5或7 D、5或6或74. 如图所示 , □ABCD的面积是12,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( ) A、2 B、3 C、4 D、65. 如图,在▱ABCD中,对角线AC,BD交于点O,点E是BC的中点。若OE=3cm,则AB的长为( )
A、2 B、3 C、4 D、65. 如图,在▱ABCD中,对角线AC,BD交于点O,点E是BC的中点。若OE=3cm,则AB的长为( ) A、3cm B、6cm C、9cm D、12cm6. 如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的有( )
A、3cm B、6cm C、9cm D、12cm6. 如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的有( )
①图甲,DE⊥AC,BF⊥AC;②图乙,DE平分∠ADC,BF平分∠ABC;③图丙,E是AB的中点,F是CD的中点;④图丁,E是AB上一点,EF⊥AB。
A、3个 B、4个 C、1个 D、2个7. 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AB=BC=5,BD=7,则Rt△ADC的周长为( ) A、5 B、7 C、9 D、128. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°, , 则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ,正确的个数是( )
A、5 B、7 C、9 D、128. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°, , 则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ,正确的个数是( )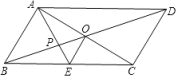 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 如图,五边形 中, ,则 的度数是.
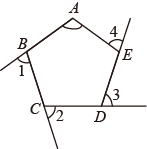 10. 在 中, ,则 的度数是.11. 如图,活动衣架可以伸缩自如,是利用了四边形的 性质.
10. 在 中, ,则 的度数是.11. 如图,活动衣架可以伸缩自如,是利用了四边形的 性质. 12. 在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为 .13. 如图,平行四边形 的周长为 , 的周长为 ,则对角线 的长为 .
12. 在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为 .13. 如图,平行四边形 的周长为 , 的周长为 ,则对角线 的长为 . 14. 在平行四边形ABCD中,对角线AC长为8cm, , , 则它的面积为cm2 .15. 如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点。若AC+BD=24cm,△OAB的周长是20cm,则EF=cm。
14. 在平行四边形ABCD中,对角线AC长为8cm, , , 则它的面积为cm2 .15. 如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点。若AC+BD=24cm,△OAB的周长是20cm,则EF=cm。 16. 在平行四边形 中, , ,将 沿对角线 翻折至 ,连接 .若 ,则点C到 边的距离为.
16. 在平行四边形 中, , ,将 沿对角线 翻折至 ,连接 .若 ,则点C到 边的距离为.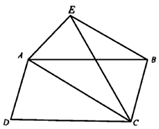
三、作图题
-
17. 如图,平面直角坐标系中点D坐标为(1,1),每个小正方形网格的顶点叫做格点,平行四边形ABCD的顶点均在格点上.仅用无刻度直尺在给定网格中按要求作图,作图过程用虚线表示,作图结果用实线表示.
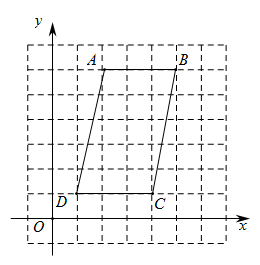
⑴将线段AD绕点A逆时针旋转90°,画出对应线段AE,并直接写出点E的坐标 ▲▲ ;
⑵过(1)中点E画一条直线把平行四边形ABCD分成面积相等的两部分;
⑶找一个格点F,使得CF⊥AD,并直接写出点F的坐标 ▲ .
四、解答题
-
18. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
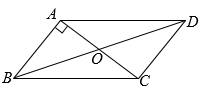 19. 如图所示,一块较为精密的模板中,AB,CD的延长线应该相交成80°的角,因交点不在模板上,不便测量,测得∠BAE=124°,∠DCF=155°,AE⊥EF,CF⊥EF,此时AB,CD的延长线相交成的角是否符合规定?为什么?
19. 如图所示,一块较为精密的模板中,AB,CD的延长线应该相交成80°的角,因交点不在模板上,不便测量,测得∠BAE=124°,∠DCF=155°,AE⊥EF,CF⊥EF,此时AB,CD的延长线相交成的角是否符合规定?为什么? 20. 如图,平行四边形ABCD中E,F是直线AC上两点,且AE=CF.求证:BE∥DF.
20. 如图,平行四边形ABCD中E,F是直线AC上两点,且AE=CF.求证:BE∥DF. 21. 如图
21. 如图 (1)、如图1,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数;(2)、如图2,求∠1+∠2+∠3+∠4+∠5+∠6的度数。
(1)、如图1,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数;(2)、如图2,求∠1+∠2+∠3+∠4+∠5+∠6的度数。五、综合题
-
22. 如图,已知▱ABCD,E为BC边上的垂直平分线,BF=BC=2AB,且∠ABD=90°.
 (1)、求证:△ABD≌△CEF;(2)、连接AF,请判断四边形ABDF的形状,并说明理由.23. 如图,四边形ABCD为平行四边形,E为AD上的一点,连结EB并延长至点F,使BF=BE,连结EC并延长至点G,使CG=CE,连结FG.H为FG的中点,连结DH,AF。
(1)、求证:△ABD≌△CEF;(2)、连接AF,请判断四边形ABDF的形状,并说明理由.23. 如图,四边形ABCD为平行四边形,E为AD上的一点,连结EB并延长至点F,使BF=BE,连结EC并延长至点G,使CG=CE,连结FG.H为FG的中点,连结DH,AF。 (1)、求证:四边形AFHD为平行四边形;(2)、若CB=CE,∠EBC=75°,∠DCE=10°,求∠DAB的度数。24. 已知:如图,在ABCD中,对角线AC,BD相交于点O,点E,F在AC上,点G,H在BD上,且AE=CF,BG= DH。
(1)、求证:四边形AFHD为平行四边形;(2)、若CB=CE,∠EBC=75°,∠DCE=10°,求∠DAB的度数。24. 已知:如图,在ABCD中,对角线AC,BD相交于点O,点E,F在AC上,点G,H在BD上,且AE=CF,BG= DH。 (1)、若AC=6,BD=8,试求AD的取值范围;(2)、若AC=AD,∠CAD=50°,试求∠ABC的度数;(3)、求证:四边形EHFG是平行四边形。25. 在平面直角坐标系 中,对于点 与 ,给出如下的定义:
(1)、若AC=6,BD=8,试求AD的取值范围;(2)、若AC=AD,∠CAD=50°,试求∠ABC的度数;(3)、求证:四边形EHFG是平行四边形。25. 在平面直角坐标系 中,对于点 与 ,给出如下的定义:将过点 的直线记为 ,若直线 与 有且只有两个公共点,则称这两个公共点之间的距离为直线 与 的“穿越距离”,记作 .
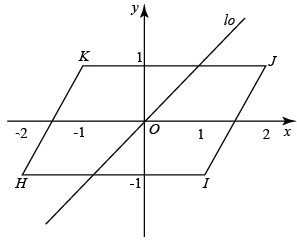
例如,已知过点 的直线 与 ,其中 , , , ,如图所示,则 .
请解决下面的问题:
已知 ,其中 , , , .
(1)、当 时,已知 , 为过点 的直线 .①当 时, _ ▲ ;当 时, ▲ ;
②若 ,结合图象,求 的值;
(2)、已知 , 为过点 的直线,若 有最大值,且最大值为 ,直接写出 的取值范围.
-