初中数学北师大版八年级下册第六章第三节 三角形中位线 同步练习
试卷更新日期:2022-03-04 类型:同步测试
一、单选题
-
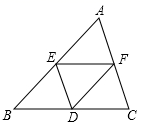
1. Rt△ABC两直角边的长分别为6cm和8cm,则连接这两条直角边中点的线段长为( )A、10cm B、3cm C、4cm D、5cm2. 如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
 A、20 B、15 C、10 D、53. 如图,在△ABC中,延长BC至点D,使得CD= BC,过AC的中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连结DF.若AB=8,则DF的长为( )
A、20 B、15 C、10 D、53. 如图,在△ABC中,延长BC至点D,使得CD= BC,过AC的中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连结DF.若AB=8,则DF的长为( )
 A、3 B、4 C、2 D、34. 如图,在△ABC中,∠ABC=90°,AC=18,BC=14,D,E分别是AB,AC的中点,连接DE,BE,点M在CB的延长线上,连接DM,若∠MDB=∠A,则四边形DMBE的周长为( )
A、3 B、4 C、2 D、34. 如图,在△ABC中,∠ABC=90°,AC=18,BC=14,D,E分别是AB,AC的中点,连接DE,BE,点M在CB的延长线上,连接DM,若∠MDB=∠A,则四边形DMBE的周长为( ) A、16 B、24 C、32 D、405. 如图,在平行四边形 中, ,点 , 分别是 , 的中点,则 等于( )
A、16 B、24 C、32 D、405. 如图,在平行四边形 中, ,点 , 分别是 , 的中点,则 等于( ) A、2 B、3 C、4 D、66. 如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有( )
A、2 B、3 C、4 D、66. 如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有( )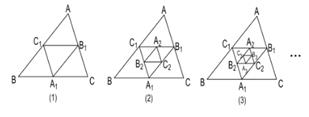 A、3个 B、4n个 C、3n个 D、3n个7. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )
A、3个 B、4n个 C、3n个 D、3n个7. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )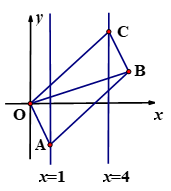 A、3 B、4 C、5 D、68. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OA,OB,CD的中点,EG交FD于点H.则下列结论:①ED⊥CA;②EF=CG;③EH= EG;④S△EFD=S△CEG成立的个数有( )
A、3 B、4 C、5 D、68. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OA,OB,CD的中点,EG交FD于点H.则下列结论:①ED⊥CA;②EF=CG;③EH= EG;④S△EFD=S△CEG成立的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图,D,E,F分别为△ABC三边的中点,则图中平行四边形的个数为.
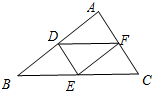 10. 如图,四边形ABCD中,AD∥BC,AD= BC,CD=BC,点E,F分别是BD,CD的中点,连接AE,EF,若BC=2,则四边形AEFD的周长为 .
10. 如图,四边形ABCD中,AD∥BC,AD= BC,CD=BC,点E,F分别是BD,CD的中点,连接AE,EF,若BC=2,则四边形AEFD的周长为 .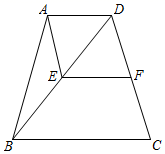 11. 如图,在Rt△ABC中,∠B=90°,AB=2 , BC=3,D,E分别是AB,AC的中点,延长BC至点F,使CF=BC,连结DF,EF,则EF的长为。
11. 如图,在Rt△ABC中,∠B=90°,AB=2 , BC=3,D,E分别是AB,AC的中点,延长BC至点F,使CF=BC,连结DF,EF,则EF的长为。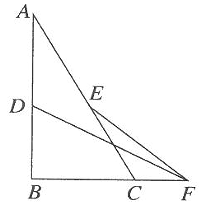 12. 如图,点 , 分别是 的边 , 的中点,连接 ,过点 作 ,交 的延长线于点 .若EF=6,则 的长为.
12. 如图,点 , 分别是 的边 , 的中点,连接 ,过点 作 ,交 的延长线于点 .若EF=6,则 的长为. 13. 如图,在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G , 若BE=8,则GE= .
13. 如图,在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G , 若BE=8,则GE= .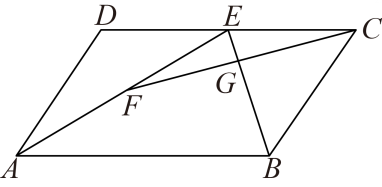 14. 如图,在四边形ABDC中,E、F、G、H分别为AB、BC、CD、DA的中点,并且E、F、G、H四点不共线.当AC=6,BD=8时,四边形EFGH的周长是 .
14. 如图,在四边形ABDC中,E、F、G、H分别为AB、BC、CD、DA的中点,并且E、F、G、H四点不共线.当AC=6,BD=8时,四边形EFGH的周长是 .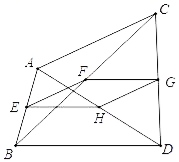 15. 有一边长为 的等边 游乐场,某人从边 中点 出发,先由点 沿平行于 的方向运动到 边上的点 ,再由 沿平行于 方向运动到 边上的点 ,又由点 沿平行于 方向运动到 边上的点 ,则此人至少要运动 ,才能回到点 .如果此人从 边上意一点出发,按照上面的规律运动,则此人至少走 ,就能回到起点.
15. 有一边长为 的等边 游乐场,某人从边 中点 出发,先由点 沿平行于 的方向运动到 边上的点 ,再由 沿平行于 方向运动到 边上的点 ,又由点 沿平行于 方向运动到 边上的点 ,则此人至少要运动 ,才能回到点 .如果此人从 边上意一点出发,按照上面的规律运动,则此人至少走 ,就能回到起点.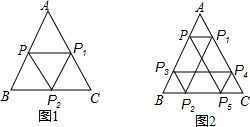 16. 如图,已知 ,点 在边 上, ,过点 作 于点 ,以 为一边在 内作等腰直角三角形 ,点 是 围成的区域(不包括各边)内的一点,过点 作 交 于点 ,作 交 于点 ,设 ,则 取值范围是.
16. 如图,已知 ,点 在边 上, ,过点 作 于点 ,以 为一边在 内作等腰直角三角形 ,点 是 围成的区域(不包括各边)内的一点,过点 作 交 于点 ,作 交 于点 ,设 ,则 取值范围是.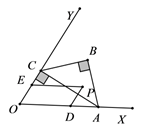
三、解答题
-
17. 证明三角形中位线定理:三角形两边中点的连线平行于第三边且等于第三边的一半.
(要求:画出图形,写出已知、求证和证明过程)
18. 如图,在△ABC中,点D,E分别是边BC,AC的中点,连结DE,AD,点F在BA的延长线上,且AF=AB,连结EF,判断四边形ADEF的形状,并加以证明。 19. 如图所示,已知AD是 的中线,DE∥AB,且DE=AB,连结AE,EC.求证:四边形ADCE是平行四边形.
19. 如图所示,已知AD是 的中线,DE∥AB,且DE=AB,连结AE,EC.求证:四边形ADCE是平行四边形. 20. 的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证: ,且 .
20. 的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证: ,且 . 21. 如图,点D、E、F分别是AC、BC、AB中点,且 BD是△ABC的角平分线.求证:BE=AF.
21. 如图,点D、E、F分别是AC、BC、AB中点,且 BD是△ABC的角平分线.求证:BE=AF.
四、综合题
-
22. 如图1,在四边形 中, 、 、 、 分别是 、 、 、 的中点.

 (1)、求证:四边形 是平行四边形;(2)、如图2,延长 、 相交于点 ,连接 、 、 ,若 ,求四边形 的面积.23. 已知,在 中, ,D是平面上一点,连接 ,把 绕点A逆时针旋转至点E,使 .连接 并延长,交 于点O,交 于点F.连接 和 , 的延长线分别交 , 于点P,G.
(1)、求证:四边形 是平行四边形;(2)、如图2,延长 、 相交于点 ,连接 、 、 ,若 ,求四边形 的面积.23. 已知,在 中, ,D是平面上一点,连接 ,把 绕点A逆时针旋转至点E,使 .连接 并延长,交 于点O,交 于点F.连接 和 , 的延长线分别交 , 于点P,G. (1)、如图1,求证: ;(2)、如图2,若点F是 的中点, ,求证 ;(3)、在(2)的条件下,若G是 的中点,连接 .当 时,请直接写出 的周长.24. (问题情境)
(1)、如图1,求证: ;(2)、如图2,若点F是 的中点, ,求证 ;(3)、在(2)的条件下,若G是 的中点,连接 .当 时,请直接写出 的周长.24. (问题情境)如图1,在 中, ,D是 边上一点,过点D作 交 于点E,以D为顶点, 为一边作 ,使其另一边与 边交于点F, 与 交于点G.
 (1)、求证:G是 的中点;(2)、M,N分别是 , 的中点,连接 ,求证:点G在线段 上;(3)、(迁移拓展)
(1)、求证:G是 的中点;(2)、M,N分别是 , 的中点,连接 ,求证:点G在线段 上;(3)、(迁移拓展)如图2,已知D是长为4的线段 上的动点(D不与A,B重合),分别以 , 为边在线段 的同侧作等边 和等边 ,G为 的中点,连接 .
①请直接写出 的最小值;(不要求写解题过程)
②请写出解题过程中需要的辅助线作法,并在图2中画出相应的辅助线.