湖北省黄石市有色一中2021年六月中考模拟考试数学试题卷
试卷更新日期:2022-03-04 类型:中考模拟
一、单选题
-
1. -2021的绝对值是( )A、﹣2021 B、 C、 D、20212. 如图所示几何体的左视图正确的是( )
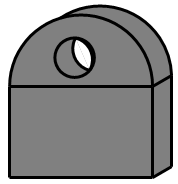 A、
A、 B、
B、 C、
C、 D、
D、 3. 在下列图形中,既是轴对称图形,又是中心对称图形的是( )A、等腰三角形 B、平行四边形 C、正三角形 D、圆4. 下列运算中,正确的是( )A、2a+3a=5a B、a6÷a3=a2 C、(a﹣b)2=a2﹣b2 D、5. 使代数式 有意义的x的取值范围是( )A、 B、 C、 且 D、6. 下列说法正确的是( )A、九年级某班的英语测试平均成绩是98.5,说明每个同学的得分都是98.5分 B、数据4,4,5,5,0的中位数和众数都是5 C、要了解一批日光灯的使用寿命,应采用全面调查 D、若甲、乙两组数据中各有20个数据,两组数据的平均数相等,方差S甲2=1.25,S乙2=0.96,则说明乙组数数据比甲组数据稳定7. 如图,在平面直角坐标系xOy中,直线 经过点A,作AB⊥x轴于点B,将△ABO绕点B顺时针旋转60°得到△BCD,若点B的坐标为(2,0),则点C的坐标为( )
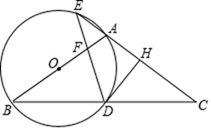
3. 在下列图形中,既是轴对称图形,又是中心对称图形的是( )A、等腰三角形 B、平行四边形 C、正三角形 D、圆4. 下列运算中,正确的是( )A、2a+3a=5a B、a6÷a3=a2 C、(a﹣b)2=a2﹣b2 D、5. 使代数式 有意义的x的取值范围是( )A、 B、 C、 且 D、6. 下列说法正确的是( )A、九年级某班的英语测试平均成绩是98.5,说明每个同学的得分都是98.5分 B、数据4,4,5,5,0的中位数和众数都是5 C、要了解一批日光灯的使用寿命,应采用全面调查 D、若甲、乙两组数据中各有20个数据,两组数据的平均数相等,方差S甲2=1.25,S乙2=0.96,则说明乙组数数据比甲组数据稳定7. 如图,在平面直角坐标系xOy中,直线 经过点A,作AB⊥x轴于点B,将△ABO绕点B顺时针旋转60°得到△BCD,若点B的坐标为(2,0),则点C的坐标为( ) A、(5, ) B、(5,1) C、(6, ) D、(6,1)8. 如图,点A,B,C在⊙O上,若 , ,则图中阴影部分的面积为( )
A、(5, ) B、(5,1) C、(6, ) D、(6,1)8. 如图,点A,B,C在⊙O上,若 , ,则图中阴影部分的面积为( ) A、 B、 C、 D、9. 已知,在△ABC中, ,如图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D; (2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中错误的是( )
A、 B、 C、 D、9. 已知,在△ABC中, ,如图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D; (2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中错误的是( ) A、 B、△BCD是等边三角形 C、AD垂直平分BC D、10. 已知二次函数 的图象经过 与 两点,关于x的方程 有两个根,其中一个根是3.则关于x的方程 有两个整数根,这两个整数根是( )A、-2或0 B、-4或2 C、-5或3 D、-6或4
A、 B、△BCD是等边三角形 C、AD垂直平分BC D、10. 已知二次函数 的图象经过 与 两点,关于x的方程 有两个根,其中一个根是3.则关于x的方程 有两个整数根,这两个整数根是( )A、-2或0 B、-4或2 C、-5或3 D、-6或4二、填空题
-
11. 计算: =.12. 分解因式: .13. 新型冠状病毒属于冠状病毒科,病毒粒子呈球形,直径为0.00000012m,用科学记数法表示m.14. 如果不等式组 的解集是 ,那么 的值为 .15. 如图是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米.(结果精确到0.1米,参考数据: ≈1.41, ≈1.73)
 16. 已知点 , ,在x轴上的点C,使得 最小,则点C的横坐标为.17. 已知Rt△ABC,且∠A=30°,若△ABC的三个顶点均在双曲线 ( >0)上,斜边AB经过坐标原点,且B点的纵坐标比横坐标少3的单位长度,C点的纵坐标与B点横坐标相等,则k=.
16. 已知点 , ,在x轴上的点C,使得 最小,则点C的横坐标为.17. 已知Rt△ABC,且∠A=30°,若△ABC的三个顶点均在双曲线 ( >0)上,斜边AB经过坐标原点,且B点的纵坐标比横坐标少3的单位长度,C点的纵坐标与B点横坐标相等,则k=.
 18. 如图,在正方形ABCD中,E是对角线BD上一点 ,将线段CE绕点C按顺时针方向旋转 得到线段 ,连接 , , .下列结论:①若 ,则 ;② ;③若 ,则 ;④若 , ,则 .其中正确的结论有(填正确的序号)
18. 如图,在正方形ABCD中,E是对角线BD上一点 ,将线段CE绕点C按顺时针方向旋转 得到线段 ,连接 , , .下列结论:①若 ,则 ;② ;③若 ,则 ;④若 , ,则 .其中正确的结论有(填正确的序号)
三、解答题
-
19. 先化简,再求值:(1+ )÷ ,其中a是满足﹣1≤a≤2的整数.20. 如图,在 中, , , ,垂足为G,且 , ,其两边分别交AB,AC于点E,F.
 (1)、若 ,求AC的长;(2)、求证: .21. 在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档: ;B档: ;C档: ;D档: .根据调查情况,给出了部分数据信息:
(1)、若 ,求AC的长;(2)、求证: .21. 在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档: ;B档: ;C档: ;D档: .根据调查情况,给出了部分数据信息:①A档和D档的所有数据是:7,7,7.5,10,7,10,7,7.5,7,7,10.5,10.5;
②图1和图2是两幅不完整的统计图.
根据以上信息解答问题:
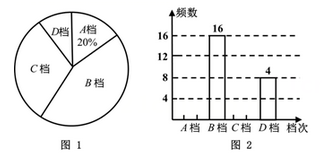 (1)、求本次调查的学生人数,并将图2补充完整;(2)、已知全校共1200名学生,请你估计全校B档的人数;(3)、学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.22. 分已知关于x的一元二次方程(m-2)x2+(2m+1)x+m=0有两个实数根x1 , x2.(1)、求m的取值范围.(2)、若|x1|=|x2|,求m的值及方程的根.23. 某社区计划对面积为 的区域进行绿化;经招标,甲、乙两个工程队中标,全部绿化工作由甲、乙两队来完成;已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为 区域的绿化时,甲队比乙队少用4天;(1)、求甲、乙两队每天能完成绿化的面积;(2)、若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,如果施工总费用不超过10.4万元,那么乙队至少需施工多少天?
(1)、求本次调查的学生人数,并将图2补充完整;(2)、已知全校共1200名学生,请你估计全校B档的人数;(3)、学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.22. 分已知关于x的一元二次方程(m-2)x2+(2m+1)x+m=0有两个实数根x1 , x2.(1)、求m的取值范围.(2)、若|x1|=|x2|,求m的值及方程的根.23. 某社区计划对面积为 的区域进行绿化;经招标,甲、乙两个工程队中标,全部绿化工作由甲、乙两队来完成;已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为 区域的绿化时,甲队比乙队少用4天;(1)、求甲、乙两队每天能完成绿化的面积;(2)、若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,如果施工总费用不超过10.4万元,那么乙队至少需施工多少天?