浙江省绍兴市上虞区2021-2022学年七年级上学期期末数学试卷

试卷更新日期：2022-03-04 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣2的相反数是（　　）

A、﹣ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、2 D、﹣2

查看试题解析
2. 2021年10月16日0时23分，翟志刚、王亚平、叶光富3名航天员搭载神舟十三号载人飞船进入太空，开启为期6个月的飞行任务.预计在太空停留约15800000秒，数据15800000用科学记数法表示正确的是（）

A、158×10⁵ B、1.58×10⁶ C、1.58×10⁷ D、0.158×10⁸

查看试题解析
3. 下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个角的是（）

A、 B、 C、 D、

查看试题解析
4. 下列说法正确的是（）

A、4的平方根是2 B、﹣8的立方根是﹣2 C、64的立方根是±4 D、平方根是它本身的数只有0和1

查看试题解析
5. 下列说法不正确的是（）

A、 $2 a$ 是2个数a的和 B、 $2 a$ 是2和数a的积 C、 $2 a$ 是单项式 D、 $2 a$ 是偶数

查看试题解析
6. 代数式 $\frac{x}{2}$ ， $\frac{s}{t}$ ， $\frac{1}{x + y}$ ，20%•x， $\sqrt{a b}$ ， $\sqrt{2}$ ab， $\frac{2 a + b}{3}$ 中，多项式有（）个

A、0 B、1 C、2 D、3

查看试题解析
7. 方程 $\frac{3 x - 1}{3}$ ＝1﹣ $\frac{4 x - 1}{6}$ 去分母后，正确的是（）

A、2（3x﹣1）＝1﹣4x﹣1 B、2（3x﹣1）＝6﹣4x+1 C、2（3x﹣1）＝6﹣4x﹣1 D、2（3x﹣1）＝1﹣4x+1

查看试题解析
8. 把 $1 - 9$ 这 $9$ 个数填入 $3 \times 3$ 方格中，使其任意一行，任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”.它源于我国古代的“洛書”（图 $①$ ），是世界上最早的“幻方”.图 $②$ 是仅可以看到部分数值的“九宫格”，则其中 $x$ 的值为（）

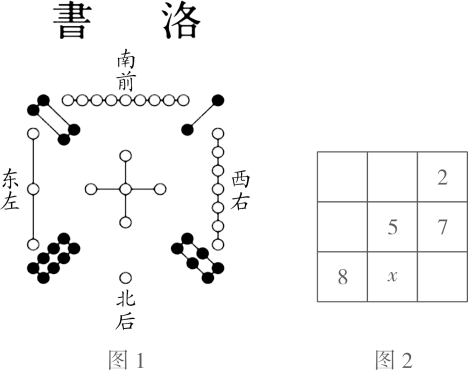A、1 B、3 C、4 D、6

查看试题解析
9. 对于任意实数a和b，如果满足 $\frac{a}{3} + \frac{b}{4} = \frac{a + b}{3 + 4} + \frac{2}{3 \times 4}$ 那么我们称这一对数a，b为“友好数对”，记为（a，b）.若（x，y）是“友好数对”，则2x﹣3[6x+（3y﹣4）]＝（）

A、﹣4 B、﹣3 C、﹣2 D、﹣1

查看试题解析
10. 如图是一纸条的示意图，第1次对折，使A，B两点重合后再打开，折痕为l₁；第2次对折，使A，C两点重合后再打开，折痕为l₂；第3次对折，使B，D两点重合后再打开，折痕为l₃.已知CE=2cm，则纸条原长为（）cm

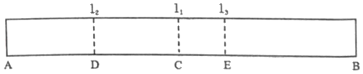A、18 B、16 C、14 D、12

查看试题解析

二、填空题

11. 比较大小： $\sqrt{5}$ 2.5.（用“＞”或“＜”或“＝”连接）

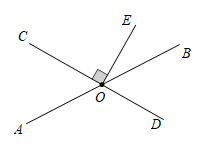
查看试题解析
12. 已知 $∠ A = 100 °$ ，则 $∠ A$ 的补角等于 $°$ ．

查看试题解析
13. 在数轴上，到﹣2的距离等于4个单位长度的点所表示的数是 .

查看试题解析
14. 代数式a﹣b，b+c，﹣（a+c）的和是 .

查看试题解析
15. 如图，直线 $A B$ ， $C D$ 相交于点 $O$ ， $O E ⊥ C D$ ，垂足为点 $O$ ，若 $∠ B O E = 40 °$ ，则 $∠ A O C$ 的度数为.

查看试题解析
16. 某种商品每件的进价为120元，标价为180元．为了拓展销路，商店准备打折销售．若使利润率为20%，则商店应打折．

查看试题解析
17. 某数学老师在课外活动中做了一个有趣的游戏：首先发给A、B、C三个同学相同数量的扑克牌 $($ 假定发到每个同学手中的扑克牌数量足够多 $)$ ，然后依次完成以下三个步骤：
第一步，A同学拿出二张扑克牌给B同学；

第二步，C同学拿出三张扑克牌给B同学；

第三步，A同学手中此时有多少张扑克牌，B同学就拿出多少张扑克牌给A同学.

请你确定，最终B同学手中剩余的扑克牌的张数为.

查看试题解析
18. 若一个小烧杯中盛有11克糖水，且糖水中含糖2克，则这一小杯糖水的质量浓度为 $\frac{2}{11}$ ，现另有4个小烧杯，杯中依次盛有b₁ ， b₂ ， b₃ ， b₄克糖水，并且糖水中分别含糖a₁ ， a₂ ， a₃ ， a₄克，现将这5杯糖水一起倒入一个足够大的空杯中

(1)、用代数式表示这一大杯糖水的质量浓度为.

(2)、若这5杯糖水的质量浓度不全相同，那么这一大杯糖水的质量浓度与 $\frac{2}{11}$ 相比是关系.（①大于；②小于；③等于；④不能确定.只须填写序号即可.）

查看试题解析

三、解答题

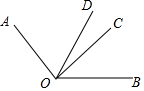
19. 计算：

(1)、4﹣3×2²；

(2)、﹣2²÷ $\frac{2}{3}$ ×（1﹣ $\frac{1}{3}$ ）².

查看试题解析
20. 解答下列各题：

(1)、化简并求值：（a﹣ab）+（b+2ab）﹣（a+b），其中a＝7，b＝﹣ $\frac{1}{7}$ .

(2)、如图，OD为∠AOB的平分线，∠AOC=2∠BOC，AO⊥CO，求∠COD的度数.

查看试题解析
21. 为庆祝伟大的中国共产党成立100周年，某校德育处举行了以“学史明理，学史增信，学史崇德，学史力行”为主题的党史知识竞赛.竞赛共有50道题，满分100分，每答对一题得2分，答错扣1分，不答得0分.

(1)、小芳同学只有一道题没有作答，最后她的总得分为86分，则她答对了多少道题？

(2)、若规定参赛者总得分90分及以上才可以被评为“学党史小达人”，小敏同学的得分正好符合评奖的最低控制分数从而被评为“学党史小达人”，则她答对了多少道题？

查看试题解析
22. 如图1将线段AB，CD放置在直线l上，点B与点C重合，AB=10cm，CD=15cm，点M是线段AC的中点，点N是线段BD的中点.解答下列问题：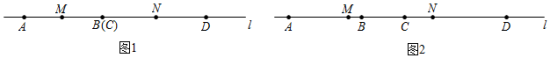

(1)、MN=

(2)、将图1中的线段AB沿DC延长线方向移动xcm至图2的位置.
①当x=7cm时，求MN的长.

②在移动的过程中，请直接写出MN，AB，CD之间的数量关系式.

查看试题解析
23. 如图，现有A，B两个圆柱形容器，B容器的底面积为S，高为18cm，A容器的底面积是B容器底面积的2倍，容器内水的高度为10cm.

(1)、若把A容器内的水全部倒入B容器中，则水溢出.（直接填“会”或“不会”即可.）

(2)、若（1）中的水会溢出，则当B容器中水倒满时，求A容器中剩余水的高度；若（1）中的水不会溢出，求此时B容器内水面的高度；

(3)、在倒水的过程中，当两个容器中水面高度相同时，求此时容器内水面的高度.

查看试题解析
24. 如图是一个运算程序的示意图.输入一个整数便能按图中程序进行计算.

(1)、设输入数x为18，那么根据程序，第1次计算的结果是9，第2次计算的结果是4…，按这样的程序计算下去，第5次计算的结果为；程序最终输出结果为

(2)、若输入某数x后，程序依次交替进行两种运算，且最后输出结果为1.请尝试通过分析，判断输入数x是奇数还是偶数？进一步借助计算，直接写出该输入数x.

查看试题解析