浙江省宁波市余姚市2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-03-04 类型:期末考试
一、单选题
-
1. 在-3,-2,0,1这四个数中最小的数是( )A、1 B、0 C、-2 D、-32. 2021年12月9日备受疗目的中国空间站第一课 “天宫课堂”,通过架设在太空3600 万米的中继卫星与地面之间顺利开讲.其中3600万用科学记数法可表示为( )A、 B、 C、 D、3. 在 (相邻两个1之间依次多一个2) 这些数中,无理数的个数有 ( )A、5 个 B、4 个 C、3 个 D、2 个4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线 与 相交于点 与 互余, ,则 的度数是( )
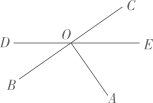 A、55° B、45° C、35° D、65°6. 下列说法:(1)在所有连结两点的线中,线段最短;(2)连接两点的线段叫做这两点的距离;(3)若线段 ,则点 是线段 的中点;(4)经过刨平的木板上的两个点,能弹出一条笔直的墨线,是因为两点确定一条直线,其中说法正确的是 ( )A、(1)(2)(3) B、(1)(4) C、(2)(3) D、(1)(2)(4)7. 我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗, 醐洒一斗直粟三斗,今持粟三斛,得酒五斗,问清跴酒各几何?”大意是:现有一斗清酒价值10斗谷子,一斗䣾酒价值3斗谷子, 现在拿30斗谷子,共换了5斗酒,问清洒, 酳酒各几斗? 如果设清酒 斗,那么可列方程为( )A、 B、 C、 D、8. 下列等式变形:(1)如果 ,那么 ;(2) 如果 , 那么 ;(3)如果 ,那么 ;(4)如果 ,那么 .其中正确的有( )A、(1)(2)(4) B、(1)(2)(3) C、(1)(3) D、(2)(4)9. 如图, 数轴上有若干个点, 每相邻两点相距1个单位长度.其中点 对应的数分 别是 ,且 和 互为相反数,则 的值为( )
A、55° B、45° C、35° D、65°6. 下列说法:(1)在所有连结两点的线中,线段最短;(2)连接两点的线段叫做这两点的距离;(3)若线段 ,则点 是线段 的中点;(4)经过刨平的木板上的两个点,能弹出一条笔直的墨线,是因为两点确定一条直线,其中说法正确的是 ( )A、(1)(2)(3) B、(1)(4) C、(2)(3) D、(1)(2)(4)7. 我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗, 醐洒一斗直粟三斗,今持粟三斛,得酒五斗,问清跴酒各几何?”大意是:现有一斗清酒价值10斗谷子,一斗䣾酒价值3斗谷子, 现在拿30斗谷子,共换了5斗酒,问清洒, 酳酒各几斗? 如果设清酒 斗,那么可列方程为( )A、 B、 C、 D、8. 下列等式变形:(1)如果 ,那么 ;(2) 如果 , 那么 ;(3)如果 ,那么 ;(4)如果 ,那么 .其中正确的有( )A、(1)(2)(4) B、(1)(2)(3) C、(1)(3) D、(2)(4)9. 如图, 数轴上有若干个点, 每相邻两点相距1个单位长度.其中点 对应的数分 别是 ,且 和 互为相反数,则 的值为( ) A、-3 B、-1 C、1 D、310. 如图,将图1中的长方形纸片前成(1)号、(2)号、(3)号、(4)号正方形和(5)号长方形,并将它们按图2的方式无重叠地放入另一个大长方形中,若需求出没有覆盖的阴影部分的周长, 则下列说法中错误的是( )
A、-3 B、-1 C、1 D、310. 如图,将图1中的长方形纸片前成(1)号、(2)号、(3)号、(4)号正方形和(5)号长方形,并将它们按图2的方式无重叠地放入另一个大长方形中,若需求出没有覆盖的阴影部分的周长, 则下列说法中错误的是( )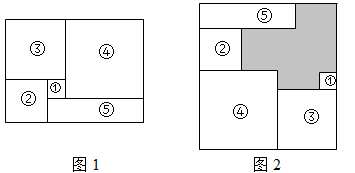 A、只需知道图 1 中大长方形的周长即可 B、只需知道图 2 中大长方形的周长即可 C、只需知道(3)号正方形的周长即可 D、只需知道(5)号长方形的周长即可
A、只需知道图 1 中大长方形的周长即可 B、只需知道图 2 中大长方形的周长即可 C、只需知道(3)号正方形的周长即可 D、只需知道(5)号长方形的周长即可二、填空题
-
11. 4的平方根是12. 单项式 的系数是 , 次数是.13. 计算: .14. 已知 ,则 .15. 钟面上4时30分,时针与分针的夹角是度,15分钟后时针与分针的夹角是度.16. 如图, 是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖, 周围是正三角形和正方形的地板砖.从里向外的第 1 层包括 6 个正方形 和 6 个正三角形,第 2 层包括 6 个正方形和 18 个正三角形, 依此递推,第 50 层中含有正三角形个数为个.

三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 先化简,再求值: ,其中 .19. 解方程:(1)、 ;(2)、 .20. 如图,长方形内有两个相邻的正方形面积分别为11和16 .
 (1)、小正方形边长的值在和这两个连续整数之间.(2)、请求出图中阴影部分的面积.21. 国庆黄金周电影《长津湖》成为了浙江人民观影的首选,宁波某区9月30日该电影票的售票量为 万张,该区10月1日到10月7日售票量的变化如下表(正号表示售票量比前一天多,负号表示售票量比前一天少):
(1)、小正方形边长的值在和这两个连续整数之间.(2)、请求出图中阴影部分的面积.21. 国庆黄金周电影《长津湖》成为了浙江人民观影的首选,宁波某区9月30日该电影票的售票量为 万张,该区10月1日到10月7日售票量的变化如下表(正号表示售票量比前一天多,负号表示售票量比前一天少):日期
1 日
2 日
3 日
4 日
5 日
6 日
7 日
售票量的变化(单位:万张)
+0.5
+0.1
-0.3
-0.2
+0.4
-0.2
+0.1
请根据以上信息, 回答下列问题:
(1)、10月2日的售票量为多少万张?(2)、10月7日与9月30日相比较, 哪一天的售票量多? 多多少万张?(3)、若平均每张票价为50元,则10月1日到10月7日该区销售 长津湖》电影票共收入多少万元?22. 已知线段 (如图),延长 至点 ,使 ,延长 至点 ,使 . (1)、请按上述要求画全图形;(2)、求线段 的长(用含 的代数式表示);(3)、若 是 的中点, ,求 的值.23. “水是生命之源”,某自来水公司为鼓励用户节约用水,对 “一户一表” 居民用水按以下规定收取水费:
(1)、请按上述要求画全图形;(2)、求线段 的长(用含 的代数式表示);(3)、若 是 的中点, ,求 的值.23. “水是生命之源”,某自来水公司为鼓励用户节约用水,对 “一户一表” 居民用水按以下规定收取水费:月用水量/吨
单价(元/吨)
不超过10吨的部分
2.6
超过10吨但不超过18吨的部分
3.5
超过 18 吨的部分
4.3
注意:另外每吨用水加收 元的城市污水处理费
例如:某用户11月份用水16吨,共需交纳水费为:
元.
请根据以上信息,回答下列问题:
(1)、若小聪家11月份用水12吨,那么共需交纳水费多少元?(2)、若小明家11月份共交纳水费 64.1元, 那么小明家11月份用水多少吨?(3)、若小聪和小明家12月份共用水 23 吨,共交纳水费81.8元,其中小聪家用水量少于10吨,那么小聪家和小明家12月份各用水多少吨?24. 如图1, 已知 ,射线 从 位置出发,以每秒 的速度按顺时针方向向射线 旋转;与此同时, 射线 以每秒 的速度,从 位置出发按逆时针方向向射线 旋转,到达射线 后又以同样的速度按顺时针方向返回,当射线 与射线 重合时,两条射线同时停止运动,设旋转时间为t(s).
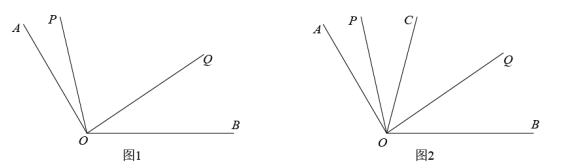 (1)、当 时, 求 的度数;(2)、当 与 重合时,求 的值;(3)、如图2,在旋转过程中, 若射线 始终平分 ,问:是否存在 的值, 使得 若存在,请直接写出 的值;若不存在,请说明理由.
(1)、当 时, 求 的度数;(2)、当 与 重合时,求 的值;(3)、如图2,在旋转过程中, 若射线 始终平分 ,问:是否存在 的值, 使得 若存在,请直接写出 的值;若不存在,请说明理由.