浙江省丽水市缙云县2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-03-04 类型:期末考试
一、单选题
-
1. 下列各数中,最大的数是( )A、2 B、-2 C、 D、2. 某地某天的最高气温是10℃,最低气温是-1℃,则该地这一天的温差是( )A、11℃ B、-9℃ C、9℃ D、-10℃3. 习近平总书记提出了未来5年“精准扶贫”的战略构想,意味着每年要减贫约11700000人,将数据11700000用科学记数法表示为( )A、1.17×106 B、1.17×107 C、1.17×108 D、11.7×1064. 在实数:0, , , , 0.020020002…(每两个2之间零的个数依次增加1)中,无理数有( )A、1个 B、2个 C、3个 D、4个5. 下列运算正确的是( )A、 B、 C、 D、6. 已知关于x的方程 的解是 ,则a的值为( )A、2 B、3 C、4 D、57. 如图,点A表示的实数是a , 则下列判断正确的是( )
 A、 B、 C、 D、8. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间9. 如图,在编写数学谜题时,“□”表示同一个数字,若设“□”为y,则列出的方程正确的是( )
A、 B、 C、 D、8. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间9. 如图,在编写数学谜题时,“□”表示同一个数字,若设“□”为y,则列出的方程正确的是( )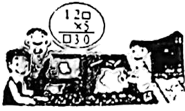 A、 B、 C、 D、10. 将一副直角三角尺按如图所示的不同方式摆放,则图中∠α与∠β相等的是( )
A、 B、 C、 D、10. 将一副直角三角尺按如图所示的不同方式摆放,则图中∠α与∠β相等的是( )
A、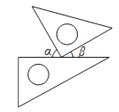 B、
B、 C、
C、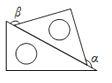 D、
D、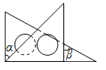
二、填空题
-
11. 一袋糖果包装上印有总质量 .小明拿去称了一下,发现质量为497g,则该袋糖果是否合格(填“是”或“否”).12. 请写出一个解为4的一个一元一次方程 .13. 用代数式表示“x的4倍与3的差”,结果为.14. 已知 ,则 的余角的度数是.15. 若代数式 的值是 ,则代数式 的值为.16. 如图,某学校图书馆把Wifi密码做成了数学题.小红在图书馆看书时,思索了一会儿,输入密码,顺利地连接到了“图书馆”的网络.那么她输入的密码是.

三、解答题
-
17. 计算:(1)、-9+5+3;(2)、 .18. 先化简,再求值: ,其中 .19. 如图,已知直线BC及直线外一点A,按要求完成下列问题:
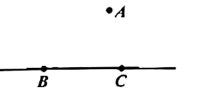 (1)、画出射线CA,线段AB,过C点画CD⊥AB,垂足为点D;(2)、比较线段CD和线段CA的大小,并说明理由.20. 小慧解方程 的过程如下所示:
(1)、画出射线CA,线段AB,过C点画CD⊥AB,垂足为点D;(2)、比较线段CD和线段CA的大小,并说明理由.20. 小慧解方程 的过程如下所示:解:去分母,得 ①
去括号,得 ②
移项,得 ③
合并同类项,得 ④
两边同除以7,得 ⑤
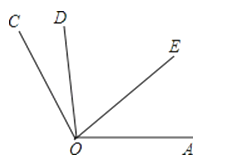
(1)、她解答过程中错误的步骤是;(2)、请写出正确的解答过程.21. 如图,OE为∠AOD的平分线,∠COD=∠EOC,∠COD=15°,求:①∠EOC的大小; ②∠AOD的大小.
 22. 如图,点C为线段AB上一点,线段AC与CB的长度之比为3:4,D为线段AC的中点.
22. 如图,点C为线段AB上一点,线段AC与CB的长度之比为3:4,D为线段AC的中点. (1)、若AB=28,求BD的长;(2)、画出线段BD的中点E,若CE=a,求AB的长(用含a的代数表示).23. 盲盒近来火爆,这种不确定的“盲盒”模式受到了大家的喜爱,某玩具商店计划采购文具盲盒和Molly盲盒,计划采购两种盲盒共100盒,这两种盲盒的进价、售价如表所示:
(1)、若AB=28,求BD的长;(2)、画出线段BD的中点E,若CE=a,求AB的长(用含a的代数表示).23. 盲盒近来火爆,这种不确定的“盲盒”模式受到了大家的喜爱,某玩具商店计划采购文具盲盒和Molly盲盒,计划采购两种盲盒共100盒,这两种盲盒的进价、售价如表所示:类型
进价(元/盒)
售价(元/盒)
文具盲盒
16
20
Molly盲盒
36
52
(1)、若采购共用去3400元,则两种盲盒各采购了多少盒?(2)、在(1)的条件下全部售完这100盒,那么玩具商店获利多少元?(3)、是否有一种采购方案使得销售完这100盒盲盒的总利润恰好为1400元?若能,请说出采购方案;若不能,证明理由.24. 【阅读理解】规定:我们把若干个相同的有理数(不为0)的除法运算叫做除方,如 , 等.类比有理数的乘方,我们把 ,记作 ,读作“2的圈3次方”, 记作 ,读作“-3的圈4次方”.一般地,把 记作 作“a的圈n次方”.(1)、【初步探究】直接写出计算结果: = , =;(2)、【类比探究】我们知道,有理数的减法运算转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?试一试:仿照如图所示的算式,将下列运算结果直接写成乘方的形式: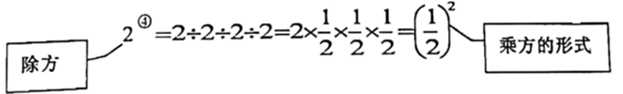
=; =.
(3)、【深入思考】想一想:将一个非零有理数a的圈n次方写成乘方的形式是.(4)、【综合运用】算一算: (约定:除方和乘方是同级运算)