广西壮族自治区百色市靖西市2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-03-04 类型:期末考试
一、单选题
-
1. -8的绝对值等于( )A、8 B、-8 C、 D、2. 下列四个角中,钝角是( )A、
 B、
B、 C、
C、 D、
D、 3. 想表示某种品牌奶粉中蛋白质、钙、维生素、糖、其它物质的含量的百分比,应该利用( ):A、条形统计图 B、扇形统计图 C、折线统计图 D、以上都可以4. 下列几何体中,面的个数最多的是( )A、
3. 想表示某种品牌奶粉中蛋白质、钙、维生素、糖、其它物质的含量的百分比,应该利用( ):A、条形统计图 B、扇形统计图 C、折线统计图 D、以上都可以4. 下列几何体中,面的个数最多的是( )A、 B、
B、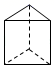 C、
C、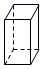 D、
D、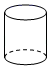 5. 2021年2月10日19时52分,中国首次火星探测任务“天问一号”探测器成功“刹车”被火星“捕获”.在制动捕获过程中,探测器距离地球的距离为192000000公里.数字192000000用科学记数法表示为( )A、 19.2×107 B、19.2×108 C、1.92×108 D、1.92×1096. 已知方程(m﹣1)x|m|=6是关于x的一元一次方程,则m的值是( )A、±1 B、1 C、0或1 D、﹣17. 观察如图所示的程序,若输出的结果为3,则输入的x值为( )
5. 2021年2月10日19时52分,中国首次火星探测任务“天问一号”探测器成功“刹车”被火星“捕获”.在制动捕获过程中,探测器距离地球的距离为192000000公里.数字192000000用科学记数法表示为( )A、 19.2×107 B、19.2×108 C、1.92×108 D、1.92×1096. 已知方程(m﹣1)x|m|=6是关于x的一元一次方程,则m的值是( )A、±1 B、1 C、0或1 D、﹣17. 观察如图所示的程序,若输出的结果为3,则输入的x值为( ) A、1 B、﹣2 C、﹣1或2 D、1或28. 下列说法正确的是( )A、射线 与射线 是同一条射线 B、射线 的长度是 C、直线 , 相交于点 D、两点确定一条直线9. 若单项式2am+6b2n+1与a5b7的和仍是单项式,则m+n的值为( ).A、-4 B、4 C、-2 D、210. 为了解我县七年级2600名学生的视力情况,从中抽取了500名学生,对其视力进行了统计分析,以下说法正确的是( )A、2600名学生是总体 B、每个学生是个体 C、样本容量是500 D、 名学生是总体的一个样本11. 如图,已知射线OP的端点O在直线AB上,∠AOP比∠BOP的4倍少45°,设∠AOP的度数为x°,∠BOP的度数为y°,则x,y满足的关系是( )
A、1 B、﹣2 C、﹣1或2 D、1或28. 下列说法正确的是( )A、射线 与射线 是同一条射线 B、射线 的长度是 C、直线 , 相交于点 D、两点确定一条直线9. 若单项式2am+6b2n+1与a5b7的和仍是单项式,则m+n的值为( ).A、-4 B、4 C、-2 D、210. 为了解我县七年级2600名学生的视力情况,从中抽取了500名学生,对其视力进行了统计分析,以下说法正确的是( )A、2600名学生是总体 B、每个学生是个体 C、样本容量是500 D、 名学生是总体的一个样本11. 如图,已知射线OP的端点O在直线AB上,∠AOP比∠BOP的4倍少45°,设∠AOP的度数为x°,∠BOP的度数为y°,则x,y满足的关系是( ) A、 B、 C、 D、12. 如图,正方形ABCD的边长是2个单位长度,一只乌龟(看作一点)从点A出发以2个单位长度/秒的速度绕正方形顺时针运动,另有一只兔子(看作一点)也从点A出发以6个单位长度/秒的速度绕正方形逆时针运动,1秒后乌龟运动到点D,兔子也运动到点D,记为第1次相遇,则第2022次相遇在( )
A、 B、 C、 D、12. 如图,正方形ABCD的边长是2个单位长度,一只乌龟(看作一点)从点A出发以2个单位长度/秒的速度绕正方形顺时针运动,另有一只兔子(看作一点)也从点A出发以6个单位长度/秒的速度绕正方形逆时针运动,1秒后乌龟运动到点D,兔子也运动到点D,记为第1次相遇,则第2022次相遇在( ) A、点A处 B、点B处 C、点C处 D、点D处
A、点A处 B、点B处 C、点C处 D、点D处二、填空题
-
13. 如图是某同学6次数学测验成绩的折线统计图,则该同学这6次成绩的最低分是分.
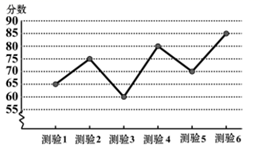 14. 已知 ∠AOB=∠COD=90°,则∠1∠2.(填“>,<,=”)
14. 已知 ∠AOB=∠COD=90°,则∠1∠2.(填“>,<,=”) 15. 鸡和兔共有100只,鸡的脚比兔的脚多20只,则鸡有只.16. 如图,已知点C为 上一点, ,D,E分别为 , 的中点,则 的长为 .
15. 鸡和兔共有100只,鸡的脚比兔的脚多20只,则鸡有只.16. 如图,已知点C为 上一点, ,D,E分别为 , 的中点,则 的长为 . 17. 北京时间21点30分,此时钟表的时针和分针构成的角度是 .18. 观察下列一组代数式:a, ,…,它们是按一定规律排列的,那么这一组数的第n个代数式为 .
17. 北京时间21点30分,此时钟表的时针和分针构成的角度是 .18. 观察下列一组代数式:a, ,…,它们是按一定规律排列的,那么这一组数的第n个代数式为 .三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 解方程:(1)、 ;(2)、 .21. 先化简,再求值: ,当 时,求代数式的值.22. 如图, 是 内的两条射线, 平分 , ,若 , ,求 的度数.
 23. 小华为了解自家小汽车的使用情况,随机选取一周,连续记录了这周的7天中她家小汽车每天行驶的路程.她的记录方法是:以 为标准,超过或不足 的部分分别用正数、负数表示.下面是她调查记录的数据(单位: ): , , , , , , .(1)、请你计算小华家小汽车这7天共行驶的路程;(2)、请你估算小华家小汽车一个月(按30天算)行驶的路程.24. 某校对本校学生进行了“写出你最喜欢的体育活动项目”(只写一项)的随机抽样调查,如图是根据得到的相关数据绘制的统计图的一部分.请根据以上信息解答下列问题:
23. 小华为了解自家小汽车的使用情况,随机选取一周,连续记录了这周的7天中她家小汽车每天行驶的路程.她的记录方法是:以 为标准,超过或不足 的部分分别用正数、负数表示.下面是她调查记录的数据(单位: ): , , , , , , .(1)、请你计算小华家小汽车这7天共行驶的路程;(2)、请你估算小华家小汽车一个月(按30天算)行驶的路程.24. 某校对本校学生进行了“写出你最喜欢的体育活动项目”(只写一项)的随机抽样调查,如图是根据得到的相关数据绘制的统计图的一部分.请根据以上信息解答下列问题: (1)、该校对多少名学生进行了抽样调查?(2)、通过计算请将图1和图2补充完整;(3)、图2中投篮所在的扇形对应的圆心角的度数是多少?(4)、若该校共有2000名学生,请利用样本数据估计全校学生中最喜欢投篮运动的人数约为多少?25. 某工厂计划生产甲、乙两种产品,已知生产每件甲产品需要3吨A种原料和2吨B种原料,生产每件乙产品需要2吨A种原料和1吨B种原料.该厂现有A种原料120吨,B种原料70吨.(1)、甲、乙两种产品各生产多少件,恰好使两种原料全部用完?(2)、在(1)的条件下,去年每件甲产品的售价为3万元,每件乙产品的售价为5万元.根据市场调研情况,今年每件乙产品售价比去年下降10%,问每件甲产品应涨价多少万元,才能使甲、乙两种产品全部出售的总销售额达到200万元?
(1)、该校对多少名学生进行了抽样调查?(2)、通过计算请将图1和图2补充完整;(3)、图2中投篮所在的扇形对应的圆心角的度数是多少?(4)、若该校共有2000名学生,请利用样本数据估计全校学生中最喜欢投篮运动的人数约为多少?25. 某工厂计划生产甲、乙两种产品,已知生产每件甲产品需要3吨A种原料和2吨B种原料,生产每件乙产品需要2吨A种原料和1吨B种原料.该厂现有A种原料120吨,B种原料70吨.(1)、甲、乙两种产品各生产多少件,恰好使两种原料全部用完?(2)、在(1)的条件下,去年每件甲产品的售价为3万元,每件乙产品的售价为5万元.根据市场调研情况,今年每件乙产品售价比去年下降10%,问每件甲产品应涨价多少万元,才能使甲、乙两种产品全部出售的总销售额达到200万元?