云南省昭通市2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-04 类型:期中考试
一、单选题
-
1. 下列各式中,正确的是( )A、 B、 C、 D、2. 下表是昆明市地图简图的一部分,表中“云南中医药大学”“昆明南站”所在的区域分别是( )
6
云池时代广场
昆明南站
7
昆明医科大学
8
云南中医药大学
云南大学
A、 , B、 , C、 , D、 ,3. 如图,以数轴的单位长线段为边做一个正方形,以数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点 , 则点表示的数是( )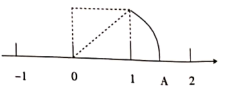 A、1.5 B、1.4 C、 D、4. 如图的四个图中,∠1与∠2是同位角的有( )
A、1.5 B、1.4 C、 D、4. 如图的四个图中,∠1与∠2是同位角的有( )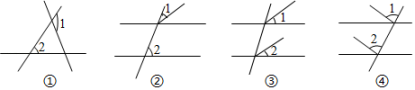 A、②③ B、①②③ C、① D、①②④5. 下列四个数中,属于无理数的是( )A、 B、 C、-1 D、6. 如图,平移△ABC得到△DEF , 其中点A的对应点是点D , 则下列结论中不成立的是( )
A、②③ B、①②③ C、① D、①②④5. 下列四个数中,属于无理数的是( )A、 B、 C、-1 D、6. 如图,平移△ABC得到△DEF , 其中点A的对应点是点D , 则下列结论中不成立的是( ) A、AD∥BE B、∠BAC=∠DFE C、AC=DF D、∠ABC=∠DEF7. 如图,下列条件中,不能判断的是( )
A、AD∥BE B、∠BAC=∠DFE C、AC=DF D、∠ABC=∠DEF7. 如图,下列条件中,不能判断的是( )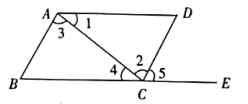 A、 B、 C、 D、8. 如图,一个机器人从点出发,向正西方向走到达点;再向正北方向走到达点 , 再向正东方向走到达点 , 再向正南方向走到达点 , 再向正西方向走到达点 , …按如此规律走下去,当机器人走到点时,点的坐标为( )
A、 B、 C、 D、8. 如图,一个机器人从点出发,向正西方向走到达点;再向正北方向走到达点 , 再向正东方向走到达点 , 再向正南方向走到达点 , 再向正西方向走到达点 , …按如此规律走下去,当机器人走到点时,点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 的相反数是.10. 如图所示,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是 .
 11. 最接近的整数是 .12. 若P(x,y)的坐标满足xy>0,且x+y<0,则点P在第象限.
11. 最接近的整数是 .12. 若P(x,y)的坐标满足xy>0,且x+y<0,则点P在第象限.
13. 把命题“直角等于90°”改写成“如果…那么…”的形式为 .14. 在平面直角坐标系中,若x轴上的点P到y轴的距离为3,则点P的坐标是 .
三、解答题
-
15. 计算: .16. 求满足下列各式的未知数 .(1)、 .(2)、 .17. 填空并完成以下证明: 已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.

证明:∵∠1=∠ACB(已知)
∴DE∥BC( ▲ )
∴∠2= ▲ ( ▲ )
∵∠2=∠3(已知)
∴∠3= ▲ (等量代换)
∴CD∥FH( ▲ )
∴∠BDC=∠BHF( ▲ )
又∵FH⊥AB(已知)
∴ ▲
18. 周末,小明、小华、小丽三名同学相约到政府广场上玩.出发前,他们每人带了一张利用平面直角坐标系画出的草图,其中市政府的坐标是 , 某酒店的坐标是 . (1)、如图,是省略了平面直角坐标系后的示意图,请你根据上述信息,画出这个被省略的平面直角坐标系;(2)、在此坐标系中,某研究所的坐标是 , 公交车站的坐标是;(3)、小华、小丽两人到了升旗台附近,这时还没有看见小明,于是打电话问小明的位置,小明说他所在位置的坐标为 .
(1)、如图,是省略了平面直角坐标系后的示意图,请你根据上述信息,画出这个被省略的平面直角坐标系;(2)、在此坐标系中,某研究所的坐标是 , 公交车站的坐标是;(3)、小华、小丽两人到了升旗台附近,这时还没有看见小明,于是打电话问小明的位置,小明说他所在位置的坐标为 .①请你在图中用字母标出小明的位置;
②过了一段时间,又打电话问小明的位置,小明说他向北走了3个单位长度,此时小明所在位置的坐标是 ▲ .


