辽宁省营口市老边区联合校2020-2021学年七年级下学期期中质量监测数学试题
试卷更新日期:2022-03-04 类型:期中考试
一、单选题
-
1. 9的算术平方根是( )A、 B、 C、3 D、-32. 下列作图能表示点A到BC的距离的是( )A、
 B、
B、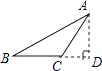 C、
C、 D、
D、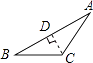 3. 下列方程:①x-2=0;②2x+y=3;③-y=2;④3xy-1=0;⑤x+=1;⑥5x-2y2=1.其中是二元一次方程的有( )A、2个 B、3个 C、4个 D、5个4. 若点在第二象限内,则应是( )A、正数 B、负数 C、非负数 D、有理数5. 在如图五幅图案中,(2)、(3)、(4)、(5)中哪一幅图案可以通过平移图案(1)得到( )
3. 下列方程:①x-2=0;②2x+y=3;③-y=2;④3xy-1=0;⑤x+=1;⑥5x-2y2=1.其中是二元一次方程的有( )A、2个 B、3个 C、4个 D、5个4. 若点在第二象限内,则应是( )A、正数 B、负数 C、非负数 D、有理数5. 在如图五幅图案中,(2)、(3)、(4)、(5)中哪一幅图案可以通过平移图案(1)得到( )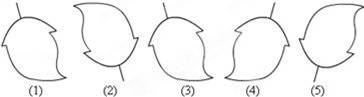 A、(2) B、(3) C、(4) D、(5)6.
A、(2) B、(3) C、(4) D、(5)6.如图,点D在直线AE上,量得∠CDE=∠A=∠C,有以下三个结论:
①AB∥CD;②AD∥BC;③∠B=∠CDA.
则正确的结论是( )
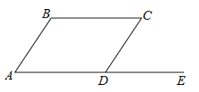 A、①②③ B、①② C、① D、②③7. 下列说法中,正确的是( )A、 与 互为相反数 B、 与 互为相反数 C、 与 互为相反数 D、 与 互为相反数8. 如图,把长方形 沿EF对折,若 ,则 的度数为( )
A、①②③ B、①② C、① D、②③7. 下列说法中,正确的是( )A、 与 互为相反数 B、 与 互为相反数 C、 与 互为相反数 D、 与 互为相反数8. 如图,把长方形 沿EF对折,若 ,则 的度数为( ) A、 B、 C、 D、9. 若a2=9, =﹣2,则a+b=( )A、﹣5 B、﹣11 C、﹣5 或﹣11 D、±5或±1110. 若点在轴上,则点的坐标为( )A、 B、 C、 D、
A、 B、 C、 D、9. 若a2=9, =﹣2,则a+b=( )A、﹣5 B、﹣11 C、﹣5 或﹣11 D、±5或±1110. 若点在轴上,则点的坐标为( )A、 B、 C、 D、二、填空题
-
11. 实数64的算术平方根是 , 平方根是 , 立方根 .12. 请写出一个以为解得二元一次方程组 .13. 比较大小:①;②;③ .14. 如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是 .
 15. 点(﹣3,5)到x轴上的距离是 , 到y轴上的距离是 .16.
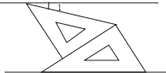
15. 点(﹣3,5)到x轴上的距离是 , 到y轴上的距离是 .16.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 .
三、解答题
-
17. 计算(1)、(2)、(3)、(4)、18. 解下列方程组(1)、(用代入法)(2)、(用加减法)(3)、(4)、19. 如图是某千年古镇的部分景点,若文昌宫的坐标为
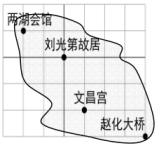 (1)、根据文昌宫的坐标“复原”平面直角坐标系;(2)、分别写出两湖会馆、刘光第故居、赵化大桥的坐标.20. 已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)、根据文昌宫的坐标“复原”平面直角坐标系;(2)、分别写出两湖会馆、刘光第故居、赵化大桥的坐标.20. 已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.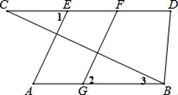 (1)、求证:AB∥CD;(2)、求∠C的度数.21. 已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1 , 它们在平面直角坐标系中的坐标如下表所示:
(1)、求证:AB∥CD;(2)、求∠C的度数.21. 已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1 , 它们在平面直角坐标系中的坐标如下表所示:△ABC
A(a,0)
B(3,0)
C(5,5)
△A1B1C1
A1(﹣3,2)
B1(﹣1,b)
C1(c,7)
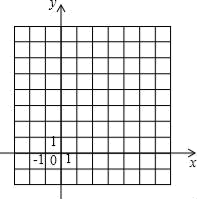 (1)、观察表中各对应点坐标的变化,并填空:a= , b= , c=;(2)、在如图的平面直角坐标系中画出△ABC及△A1B1C1;(3)、△A1B1C1的面积是.22. 平面内两条直线、相交于点 , , 恰好平分 .
(1)、观察表中各对应点坐标的变化,并填空:a= , b= , c=;(2)、在如图的平面直角坐标系中画出△ABC及△A1B1C1;(3)、△A1B1C1的面积是.22. 平面内两条直线、相交于点 , , 恰好平分 .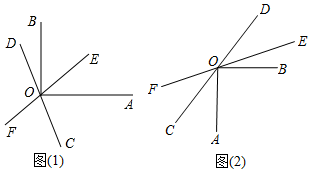 (1)、如图1,若 , 求数;(2)、在图1中,若 , 请求出的度数(用含有的式子表示),并写出和的数量关系;(3)、如图2,当 , 在直线的同侧时,和的数量关系是否会发生改变?若不变,请直接写出它们之间的数量关系;若发生变化,请说明理由.23. 如图, , . 求证: .
(1)、如图1,若 , 求数;(2)、在图1中,若 , 请求出的度数(用含有的式子表示),并写出和的数量关系;(3)、如图2,当 , 在直线的同侧时,和的数量关系是否会发生改变?若不变,请直接写出它们之间的数量关系;若发生变化,请说明理由.23. 如图, , . 求证: .
在下列解答中,填空:
证明:(已知),
①( ▲ ).
②( ▲ ).
(已知),
/③( ▲ )( ▲ ).
④( ▲ )(两直线平行,内错角相等).
⑤( ▲ ),( ▲ ),
(等量代换).
24. 列二元一次方程组解应用题一批蔬菜要运往某批发市场,菜农准备租用汽车公司的甲、乙两种货车.已知过去两次租用这两种货车的记录如下表所示:
甲种货车
(辆)
乙种货车
(辆)
总量
(吨)
第1次
4
5
28.5
第2次
3
6
27
(1)、甲、乙两种货车分别载重是多少吨?(2)、这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完,如果每吨付20元运费,问:菜农应付运费多少元?25. 如图,已知直线 , 直线和直线 , 交于点和 , 直线上有一点 .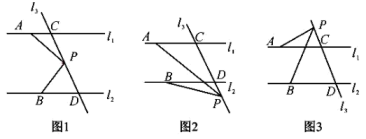 (1)、如图1,若点在 , 之间运动时,问 , , 之间的关系是否发生变化,并说明理由;(2)、若点在 , 两点的外侧运动时(点与点 , 不重合,如图2和3),试直接写出 , , 之间的关系,不必写理由.(3)、 , 时,根据(1)(2)可直接求得的度数是多少?(直接写出结果即可)
(1)、如图1,若点在 , 之间运动时,问 , , 之间的关系是否发生变化,并说明理由;(2)、若点在 , 两点的外侧运动时(点与点 , 不重合,如图2和3),试直接写出 , , 之间的关系,不必写理由.(3)、 , 时,根据(1)(2)可直接求得的度数是多少?(直接写出结果即可)