辽宁省朝阳市2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-04 类型：期中考试

进入出卷网下载

一、单选题

1. 7的平方根是（）

A、 $\pm \sqrt{7}$ B、 $\sqrt{7}$ C、 $- \sqrt{7}$ D、14

查看试题解析
2. 下列数据能确定物体具体位置的是（）

A、朝阳大道右侧 B、好运花园 $2$ 号楼 C、东经 $103 °$ ，北纬 $30 °$ D、南偏西 $55 °$

查看试题解析
3. 下列四种说法中：（1）负数没有立方根：（2）1的立方根与平方根都是1；（3） $\sqrt[3]{8}$ 的平方根是 $\pm \sqrt{2}$ ；（4） $ \sqrt[3]{8 + \frac{1}{8}} = 2 + \frac{1}{2} = 2 \frac{1}{2}$ ．其中不正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 在 $\frac{22}{7} ， \frac{π}{3} ， \sqrt{2} ， \sqrt[3]{4} ， | - \sqrt{1000} | ， - \sqrt[3]{- 9} ， \sqrt{8} ， \frac{\sqrt{5} - 1}{12} ， 1.2 \dot{3}$ ， $\sqrt[3]{216} ， 0.303003000$ …（两个“3”之间依次多一个“0”）中，无理数有（）个

A、6 B、7 C、8 D、9

查看试题解析
5. 如图，直线 $A B$ ， $C D$ 相交于点 $O$ ，射线 $O M$ 平分 $∠ B O D$ ，若 $∠ B O D = 42 °$ ，则 $∠ A O M$ 等于（）

A、 $138 °$ B、 $148 °$ C、 $159 °$ D、 $169 °$

查看试题解析
6. 下列说法正确的个数是（）
⑴没有公共点的两条直线叫做平行线；
⑵平行于同一条直线的两直线平行；
⑶经过一点有且仅有一条直线与已知直线平行；
⑷两条直线被第三条直线所截，同位角相等．

A、1 B、2 C、3 D、4

查看试题解析
7. 把点 $A (- 2 ， 3)$ 平移到点 $A^{'} (1 ， 5)$ ，平移方式正确的为（）

A、先向左平移3个单位长度，再向下平移2个单位长度 B、先向左平移3个单位长度，再向上平移2个单位长度 C、先向右平移3个单位长度，再向下平移2个单位长度 D、先向右平移3个单位长度，再向上平移2个单位长度

查看试题解析
8. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏，如图，若表示棋子“馬”和“車”的点的坐标分别为（ $3$ ， $2$ ），（﹣ $3$ ， $0$ ），则表示棋子“炮”的点的坐标为（）

A、（1，2） B、（0，2） C、（2，1） D、（2，0）

查看试题解析
9. 如图，AB和CD相交于点O，则下列结论正确的是（）

A、∠1=∠2 B、∠2=∠3 C、∠3=∠4 D、∠1=∠5

查看试题解析
10. 若点M（a+3，2a﹣4）到x轴距离是到y轴距离的2倍，则点M的坐标为（）

A、（ $\frac{20}{3}$ ， $\frac{10}{3}$ ） B、（ $\frac{20}{3}$ ， ﹣ $\frac{10}{3}$ ） C、（ $\frac{5}{2}$ ， ﹣5） D、（ $\frac{5}{2}$ ， 5）

查看试题解析

二、填空题

11. 如图，射线OC的端点O在直线AB上， $O E ⊥ O C$ 于点O，且OE平分 $∠ B O D$ ， OF平分 $∠ A O E$ ，若 $∠ B O C = 70 °$ ，则 $∠ D O F =$ ．

查看试题解析
12. 如图，直线l截直线a，b所得的8个角中，∠3的同位角是.

查看试题解析
13. 设a，b，c为不为零的实数，且 $a b c > 0$ ，那么 $x = \frac{a}{| a |} + \frac{| b |}{b} + \frac{c}{| c |}$ ，则x的值为．

查看试题解析
14. 如图，在平面直角坐标系x轴上有点 $A_{0} (1 ， 0)$ ，点 $A_{0}$ 第一次跳动至点 $A_{1} (- 1 ， 1)$ 第二次点 $A_{1}$ 跳动至点 $A_{2} (2 ， 1)$ 第三次点 $A_{2}$ 跳动至点 $A_{3} (- 2 ， 2)$ ，第四次点 $A_{3}$ 跳动至点 $A_{4} (3 ， 2)$ ， ……依此规律跳动下去，则点 $A_{2017}$ 与点 $A_{2018}$ 之间的距离是

查看试题解析
15. 如图，Rt△ABC中，AC=5，BC=12，AB=13，则其内部五个小直角三角形的周长之和为.

查看试题解析
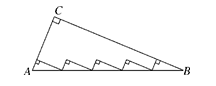16. 已知三条不同的直线a、b、c在同一平面内，下列四个命题：①如果a $/ /$ b，a⊥c，那么b⊥c；②如果b $/ /$ a，c $/ /$ a，那么b $/ /$ c；③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b $/ /$ c．其中是假命题的是．（填序号）

查看试题解析

三、解答题

17. 计算： $\sqrt{2} \times \sqrt{18} - {(- 2)}^{2} + {(2021 - π)}^{0}$

查看试题解析
18. 为了落实“村村通管道煤气”工程，煤气公司准备向村庄C铺设煤气管线，三个村庄 $A ， B ， C$ 的位置如图所示（假设煤气管线铺设线路上无任何障碍）．

(1)、若准备自村庄A向村庄C修建煤气管线，怎样铺设最节省？请你画出示意图；

(2)、若线段 $A B$ 表示的是村庄 $A ， B$ 之间铺设的煤气管线，准备从线段 $A B$ 上取一个点D，向村庄C修建一条煤气管线，怎样铺设最节省？请你画出示意图．

查看试题解析
19. 在图中，利用网格点和三角板画图或计算：

(1)、在给定方格纸中画出平移后的 $△ A^{'} B^{'} C^{'}$ ；

(2)、图中 $A C$ 与 $A^{'} C^{'}$ 的关系怎样？

(3)、记网格的边长为1，则 $△ A^{'} B^{'} C^{'}$ 的面积为多少？

查看试题解析
20. 如图， $∠ A B C + ∠ A C B = 110 °$ ， BO、CO分别平分 $∠ A B C$ 和 $∠ A C B$ ， EF过点O与BC平行，求 $∠ B O C$ ．

查看试题解析
21. 已知：如图是一个跳棋棋盘，其游戏规则是一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上例如：从起始位置 $∠ 1$ 跳到终点位置 $∠ 3$ 有两种不同路径，路径1： $∠ 1 \overset{同旁内角}{\to} ∠ 9 \overset{内错角}{\to} ∠ 3$ ；路径2： $∠ 1 \overset{内错角}{\to} ∠ 12 \overset{内错角}{\to} ∠ 6 \overset{同位角}{\to} ∠ 10 \overset{同旁内角}{\to} ∠ 3$ .
试一试：

(1)、写出从起始位置 $∠ 1$ 跳到终点位置 $∠ 8$ 的一种路径；

(2)、从起始位置 $∠ 1$ 依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点位置 $∠ 8$ ？

查看试题解析
22. 如图，已知，AB∥PF，∠FPB＝∠C，∠FED＝30°，∠AGF＝80°，FH平分∠EFG．

(1)、证明：AB∥CD；

(2)、求∠PFH的度数．

查看试题解析
23. 如图，在平面直角坐标系中，点A（0，a）、C（b，0）满足 $\sqrt{a - 2 b}$ +|b﹣2|＝0．

(1)、求点A、点C的坐标；

(2)、已知坐标轴上有两动点P、Q同时出发，P点从C点出发向左以1单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度向上移动，点D（1，2）是线段AC上一点，设运动时间为t（t＞0）秒，当S_△ODQ＝2S_△ODP时，此时是否存在点M（m，6），使得S_△ODM＝3S_△ODQ，若存在，求出点M的坐标；若不存在，请说明理由；

(3)、点F是线段AC上一点，满足∠FOC＝∠FCO，点G是第二象限中一点，连接OG，使得∠AOG＝∠AOF，点E是线段OA上一动点，连接CE交OF于点H，当点E在线段OA上运动的过程中，直接写出 $\frac{∠ O H C + ∠ A C E}{∠ O E C}$ 的值．

查看试题解析