辽宁省本溪市2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-04 类型:期中考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 为直线外一点,点 , , 为直线上三点, , , , 则到直线的距离( )A、 B、小于 C、不大于 D、3. 如图所示,过点P画直线a的平行线b的作法的依据是( )
 A、两直线平行,同位角相等 B、同位角相等,两直线平行 C、两直线平行,内错角相等 D、内错角相等,两直线平行4. 如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,∠B=40°,∠C=60°,则∠EAD的度数为( )
A、两直线平行,同位角相等 B、同位角相等,两直线平行 C、两直线平行,内错角相等 D、内错角相等,两直线平行4. 如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,∠B=40°,∠C=60°,则∠EAD的度数为( ) A、20° B、10° C、50° D、60°5. 如果是完全平方式,则k=( )A、7 B、-7 C、±7 D、7或-56. 已知 , 则的值为( )A、4 B、3 C、1 D、07. 小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图象是( )A、
A、20° B、10° C、50° D、60°5. 如果是完全平方式,则k=( )A、7 B、-7 C、±7 D、7或-56. 已知 , 则的值为( )A、4 B、3 C、1 D、07. 小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图象是( )A、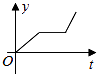 B、
B、 C、
C、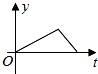 D、
D、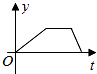 8. 下列说法正确的个数是( )
8. 下列说法正确的个数是( )①同位角的角平分线互相平行
②△ABC中,若∠C=∠A=2∠B,则△ABC是直角三角形
③周长相等的两个正方形全等
④三角形三条高线交于一点
A、1个 B、2个 C、3个 D、4个9. 如图,若 , 则下列结论一定成立的是( ) A、 B、 C、 D、10. 如图1,在长方形中,点在上, , 点从点出发,沿的路径匀速运动到点B停止,作于点Q,设点P运动的路程为x,长为y,若y与x之间的图象如图2所示,则长方形ABCD的面积为( )
A、 B、 C、 D、10. 如图1,在长方形中,点在上, , 点从点出发,沿的路径匀速运动到点B停止,作于点Q,设点P运动的路程为x,长为y,若y与x之间的图象如图2所示,则长方形ABCD的面积为( ) A、7 B、14 C、10 D、12
A、7 B、14 C、10 D、12二、填空题
-
11. 芝麻的用途广泛,经测算,一粒芝麻约有0.00000201千克.数据0.00000201用科学记数法表示为 .12. 已知一个等腰三角形的两边长分别为3和6,则该等腰三角形的周长是 .
13. 若 , , 则的值为 .14. 远通工程队承建一条长的乡村公路,预计工期为120天,若每天修建公路的长度保持不变,则还未完成的公路长度与施工时间(天)之间的关系式为 .15. 已知 , 则代数式的值为 .16. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=80°,则∠BOC= .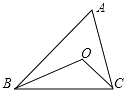 17. 若∠A的一边与∠B的一边互相平行,∠A的另一边与∠B的另一边互相垂直,且∠A=30°,则∠B的度数是 .18. 如图:的面积为 , 分别延长的三条边、、到点、、 , 使得 , , , 得到;再分别延长的三条边、、到点、、 , 使得 , , , 得到;……,按照此规律作图得到 , 则的面积 .
17. 若∠A的一边与∠B的一边互相平行,∠A的另一边与∠B的另一边互相垂直,且∠A=30°,则∠B的度数是 .18. 如图:的面积为 , 分别延长的三条边、、到点、、 , 使得 , , , 得到;再分别延长的三条边、、到点、、 , 使得 , , , 得到;……,按照此规律作图得到 , 则的面积 .
三、解答题
-
19. 计算(1)、;(2)、;(3)、 .20. 化简求值
, 其中 , .
21. 如图 , 平分 , 三点共线 , , , 求 .
解:平分 ,
( ▲ )
∴ ▲ =( ▲ )
▲ °
( ▲ )
( ▲ )
( ▲ )
▲ °
22. 某经销商销售了一种水果,根据以往销售经验,每天的售价与销售量之间有如下关系:每千克售价(元)
38
37
36
35
…
20
每天销量(千克)
50
52
54
56
…
86
(1)、上述问题中,自变量是 , 因变量是(2)、设当售价从38元/千克下调为元时,每天销售量为千克.直接写出与之间的关系式;(3)、如果这种水果的进价是20元/千克,某天的销售价定为30元/千克,这天的销售利润是多少?23. 如图,长方形的周长为16,以长方形的四条边分别为边向外作四个正方形,且这四个正方形的面积和为68,求长方形的面积. 24. 小明和爸爸到太子城运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,小明继续前行5分钟后也原路返回,两人恰好同时回家,小明和爸爸在整个运动过程中离家的距离(米)与所用时间(分)的关系如图所示:
24. 小明和爸爸到太子城运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,小明继续前行5分钟后也原路返回,两人恰好同时回家,小明和爸爸在整个运动过程中离家的距离(米)与所用时间(分)的关系如图所示: (1)、m= , n=;(2)、小明返回时和爸爸之间的距离是多少?(3)、从家出发多长时间,两人相距900米?(直接写出答案)
(1)、m= , n=;(2)、小明返回时和爸爸之间的距离是多少?(3)、从家出发多长时间,两人相距900米?(直接写出答案)

