辽宁省鞍山市铁东区2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-04 类型:期中考试
一、单选题
-
1. 9的平方根是( )A、3 B、±3 C、 D、±2. 下列数是无理数的是( )A、 B、 C、 D、3. 如图,与是( )
 A、对顶角 B、内错角 C、同位角 D、同旁内角4. 已知 A(−1,2)为平面直角坐标系中一点,下列说法正确的是( )A、点在第一象限 B、点的横坐标是 C、点到轴的距离是 D、以上都不对5. 计算:的值为( )A、 B、 C、 D、6. 如图,用方向和距离描述学校相对于小明家的位置正确的是( )
A、对顶角 B、内错角 C、同位角 D、同旁内角4. 已知 A(−1,2)为平面直角坐标系中一点,下列说法正确的是( )A、点在第一象限 B、点的横坐标是 C、点到轴的距离是 D、以上都不对5. 计算:的值为( )A、 B、 C、 D、6. 如图,用方向和距离描述学校相对于小明家的位置正确的是( ) A、学校在小明家的南偏西方向上的米处 B、学校在小明家的北偏东方向上的米处 C、学校在小明家的北偏东方向上的1200米处 D、学校在小明家的南偏西方向上的米处7. 如图,AB⊥直线l,BC⊥直线l,B为垂足,那么A,B,C三点在同一条直线上,其理由是( )
A、学校在小明家的南偏西方向上的米处 B、学校在小明家的北偏东方向上的米处 C、学校在小明家的北偏东方向上的1200米处 D、学校在小明家的南偏西方向上的米处7. 如图,AB⊥直线l,BC⊥直线l,B为垂足,那么A,B,C三点在同一条直线上,其理由是( )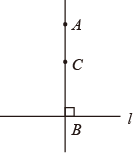 A、两点之间,线段最短 B、垂线段最短 C、在同一平面内,过一点有且只有一条直线与已知直线垂直 D、平行于同一条直线的两直线平行8. 如图, , 要证 , 需要的条件是( )
A、两点之间,线段最短 B、垂线段最短 C、在同一平面内,过一点有且只有一条直线与已知直线垂直 D、平行于同一条直线的两直线平行8. 如图, , 要证 , 需要的条件是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 把命题“邻补角互补”改写成“如果…,那么…”的形式 .10. 如果小明的座位是3组8号,记作(3,8),那么记作(2,4)表示的座位是 .11. 如图,若∠1+∠2=180°,则两条直线l1与l2的位置关系为 .
 12. 已知 ,则 .13. 如图,正方形ABCD的顶点A,D的坐标分别为(1,1),(1,4),则正方形的面积为 .
12. 已知 ,则 .13. 如图,正方形ABCD的顶点A,D的坐标分别为(1,1),(1,4),则正方形的面积为 . 14. 《九章算术》是中国传统数学名著,其中记载:“今有牛六,羊三,直金十两;牛二,羊五,直金八两.问牛,羊各直金几何?“译文:“假设有头牛,只羊,值金两;头牛,只羊,值金两.问每头牛、每只羊各值金多少两?“若设每头牛,每只羊分别值金两,两,则可列方程组为 .15. 已知关于 , 的方程组的解满足 , 则 .16. 如图所示,动点在平面直角坐标系中,按箭头所示方向呈台阶状移动,第一次从原点运动到点 , 第二次接着运动到点 , 第三次接着运动到点 , …,按这样的运动规律,经过次运动后,动点的坐标是 .
14. 《九章算术》是中国传统数学名著,其中记载:“今有牛六,羊三,直金十两;牛二,羊五,直金八两.问牛,羊各直金几何?“译文:“假设有头牛,只羊,值金两;头牛,只羊,值金两.问每头牛、每只羊各值金多少两?“若设每头牛,每只羊分别值金两,两,则可列方程组为 .15. 已知关于 , 的方程组的解满足 , 则 .16. 如图所示,动点在平面直角坐标系中,按箭头所示方向呈台阶状移动,第一次从原点运动到点 , 第二次接着运动到点 , 第三次接着运动到点 , …,按这样的运动规律,经过次运动后,动点的坐标是 .
三、解答题
-
17.(1)、计算:(2)、解方程组:(3)、解方程组:18. 如图,内有一点;
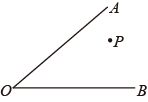 (1)、过点画直线交于点;(2)、分别过点 , 画的垂线段,垂足为 , ;(3)、请你通过测量估计与的大小的关系: . (用“”、“”、“”号填空)19. 已知:如图,直线 , 相交于点 , , 垂足为 , , 求的度数.
(1)、过点画直线交于点;(2)、分别过点 , 画的垂线段,垂足为 , ;(3)、请你通过测量估计与的大小的关系: . (用“”、“”、“”号填空)19. 已知:如图,直线 , 相交于点 , , 垂足为 , , 求的度数. 20. 已知:如图,∠1+∠B=180°,∠1=∠2.求证:AB//CD.
20. 已知:如图,∠1+∠B=180°,∠1=∠2.求证:AB//CD. 21. 如图,用两个面积为的小正方形纸片剪拼成一个大的正方形.
21. 如图,用两个面积为的小正方形纸片剪拼成一个大的正方形. (1)、大正方形的边长是;(2)、请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为的长方形纸片,使它的长宽之比为 , 若能,求出这个长方形纸片的长和宽,若不能,请说明理由.22. 有大小两种货车,辆大货车与辆小货车一次可以运货吨,辆大货车与辆小货车一次可以运货吨,求1辆大货车与1辆小货车一次共运货多少吨?23. 已知:如图,ΔABC的位置如图所示:(每个方格都是边长为个单位长度的正方形,ΔABC的顶点都在格点上),点A,B,C的坐标分别为(−1,0),(5,0),(1,5).
(1)、大正方形的边长是;(2)、请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为的长方形纸片,使它的长宽之比为 , 若能,求出这个长方形纸片的长和宽,若不能,请说明理由.22. 有大小两种货车,辆大货车与辆小货车一次可以运货吨,辆大货车与辆小货车一次可以运货吨,求1辆大货车与1辆小货车一次共运货多少吨?23. 已知:如图,ΔABC的位置如图所示:(每个方格都是边长为个单位长度的正方形,ΔABC的顶点都在格点上),点A,B,C的坐标分别为(−1,0),(5,0),(1,5). (1)、请在图中画出坐标轴,建立直角坐标系;(2)、点P(m,n)是ΔABC内部一点,平移ΔABC,点P随ΔABC一起平移,点A落在A′(0,4),点P落在P′(n,6),求点P的坐标并直接写出平移过程中线段PC扫过的面积.24. 已知:如图,直线AB//CD,直线EF交AB,CD于P,Q两点,点M,点N分别是直线CD,EF上一点(不与P,Q重合),连接PM,MN.
(1)、请在图中画出坐标轴,建立直角坐标系;(2)、点P(m,n)是ΔABC内部一点,平移ΔABC,点P随ΔABC一起平移,点A落在A′(0,4),点P落在P′(n,6),求点P的坐标并直接写出平移过程中线段PC扫过的面积.24. 已知:如图,直线AB//CD,直线EF交AB,CD于P,Q两点,点M,点N分别是直线CD,EF上一点(不与P,Q重合),连接PM,MN.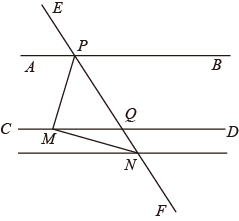
 (1)、点M,N分别在射线QC,QF上(不与点Q重合),当∠APM+∠QMN=90°时,
(1)、点M,N分别在射线QC,QF上(不与点Q重合),当∠APM+∠QMN=90°时,①试判断PM与MN的位置关系,并说明理由;
②若PA平分∠EPM,∠MNQ=20°,求∠EPB的度数.(提示:过N点作AB的平行线)
(2)、点M,N分别在直线CD,EF上时,请你在备用图中画出满足PM⊥MN条件的图形,并直接写出此时∠APM与∠QMN的关系.(注:此题说理时不能使用没有学过的定理)