上海市浦东新区第四教育署2020-2021学年九年级（下）期中数学试卷

试卷更新日期：2022-03-04 类型：期中考试

进入出卷网下载

一、单选题

1. 下列根式中，与 $\sqrt{3}$ 是同类二次根式的为（）

A、 $\sqrt{0.3}$ ； B、 $\sqrt{\frac{1}{3}}$ ； C、 $\sqrt{13}$ ； D、 $\sqrt{30}$ .

查看试题解析
2. 下列运算正确的是（）

A、 $m \cdot m = 2 m$ B、 ${(m n)}^{3} = m n^{3}$ C、 ${(m^{2})}^{3} = m^{6}$ D、 $m^{6} \div m^{2} = m^{3}$

查看试题解析
3. 二次函数y＝﹣（x﹣2）²﹣3的图象的顶点坐标是（）

A、（2，3） B、（2，﹣3） C、（﹣2，3） D、（﹣2，﹣3）

查看试题解析
4. 如图反映的是某中学九（3）班学生外出方式（乘车、步行、骑车）人数的条形统计图（部分）和扇形分布图，那么下列说法正确的是（）

A、九（3）班外出的学生共有42人 B、九（3）班外出步行的学生有8人 C、在扇形图中，步行的学生人数所占的圆心角为82° D、如果该校九年级外出的学生共有500人，那么估计全年级外出骑车的学生约有140人

查看试题解析
5. 下列图形，是轴对称图形但不是中心对称图形的是(　　)

A、线段 B、矩形 C、等腰梯形 D、圆

查看试题解析
6. 在平面直角坐标系xOy中，点A（﹣3，0），B（2，0），C（﹣1，2），E（4，2），如果△ABC与△EFB全等，那么点F的坐标可以是（　　）

A、（6，0） B、（4，0） C、（4．﹣2） D、（4，﹣3）

查看试题解析

二、填空题

7. 因式分解： $a^{2} - 4 a =$ .

查看试题解析
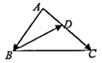
8. 计算： $a^{3} · a^{- 1} =$ ．

查看试题解析
9. 如果关于x的方程mx²﹣mx+1＝0有两个相等的实数根，那么实数m的值是．

查看试题解析
10. 已知函数f（x）＝ $\frac{2}{x^{2} + 1}$ ，那么f（﹣ $\sqrt{3}$ ）＝．

查看试题解析
11. 从1、2、3、4、5、6、7、8这八个数中，任意抽取一个数，那么抽得的数是素数的概率是．

查看试题解析
12. 某品牌旗舰店平日将某商品按进价提高40%后标价,在某次电商购物节中,为促销该商品,按标价8折销售,售价为2240元,则这种商品的进价是元.

查看试题解析
13. 已知正比例函数 $y = - 2 x$ ，那么y的值随x的值增大而（填“增大或“减小”）

查看试题解析
14. 如图，在 $△ A B C$ 中，点D在边AC上，已知 $△ A B D$ 和 $△ B C D$ 的面积比是2：3， $\vec{A B} = \vec{a} ， \vec{A C} = \vec{b}$ ，那么向量 $\vec{B D}$ （用向量 $\vec{a} ， \vec{b}$ 表示）是．

查看试题解析
15. 已知正 $n$ 边形的内角为 $140 °$ ，则 $n =$ .

查看试题解析
16. 在 $R t Δ A B C$ 中， $∠ A B C = 90 °$ ， $A B = 6$ ， $B C = 8$ ．分别以点 $A ， C$ 为圆心画圆，如果点B在⊙A上，⊙C与⊙A相交，且点A在⊙C外，那么⊙C的半径长r的取值范围是．

查看试题解析
17. 如图，梯形ABCD中，AD∥BC，∠A＝90°，它恰好能按图示方式被分割成四个全等的直角梯形，则AB：BC＝．

查看试题解析
18. 已知，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 9$ ， $B C = 12$ ，点D、E分别在边 $A C$ 、 $B C$ 上，且 $C D ： C E = 3 ： 4$ ．将 $△ C D E$ 绕点D顺时针旋转，当点C落在线段 $D E$ 上的点F处时， $B F$ 恰好是 $∠ A B C$ 的平分线，此时线段 $C D$ 的长是．

查看试题解析

三、解答题

19. 计算： $\sqrt{8} + \sqrt{2} - \sqrt{3} - \frac{1}{\sqrt{2} - 1} - 3^{\frac{1}{2}}$ ．

查看试题解析
20. 解分式方程： $\frac{x + 2}{x - 2} - \frac{16}{x^{2} - 4} = \frac{1}{x + 2}$ ．

查看试题解析
21. 如图1，一扇窗户打开一定角度，其中一端固定在窗户边OM上的点A处，另一端B在边ON上滑动，图2为某一位置从上往下看的平面图，测得∠ABO为37°，∠AOB为45°，OB长为35厘米，求AB的长（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

查看试题解析
22. 在奉贤创建文明城区的活动中，有两段长度相等的彩色道砖铺设任务，分别交给甲、乙两个施工队同时进行施工．如图是反映所铺设彩色道砖的长度y（米）与施工时间x（时）之间关系的部分图象．请解答下列问题：

(1)、求乙队在2≤x≤6的时段内，y与x之间的函数关系式；

(2)、如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加到12米/时，结果两队同时完成了任务．求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米？

查看试题解析
23. 如图，已知四边形ABCD是菱形，对角线AC、BD相交于点O，BD = 2AC．过点A作AE⊥CD，垂足为点E，AE与BD相交于点F．过点C作CG⊥AC，与AE的延长线相交于点G．

(1)、求证：△ACG≌△DOA；

(2)、求证： $D F \cdot B D = 2 D E \cdot A G$ ．

查看试题解析
24. 如图，在平面直角坐标系xOy中，抛物线y＝x²+bx经过点A（2，0）．直线y＝ $\frac{1}{2}$ x﹣2与x轴交于点B，与y轴交于点C．

(1)、求这条抛物线的表达式和顶点的坐标；

(2)、将抛物线y＝x²+bx向右平移，使平移后的抛物线经过点B，求平移后抛物线的表达式；

(3)、将抛物线y＝x²+bx向下平移，使平移后的抛物线交y轴于点D，交线段BC于点P、Q，（点P在点Q右侧），平移后抛物线的顶点为M，如果DP∥x轴，求∠MCP的正弦值．

查看试题解析
25. 已知：半圆O的直径AB＝6，点C在半圆O上，且tan∠ABC＝2 $\sqrt{2}$ ，点D为弧AC上一点，联结DC（如图）

(1)、求BC的长；

(2)、若射线DC交射线AB于点M，且△MBC与△MOC相似，求CD的长；

(3)、联结OD，当OD $/ /$ BC时，作∠DOB的平分线交线段DC于点N，求ON的长．

查看试题解析