安徽省六安市金寨县2020-2021学年九年级下学期期中数学试题
试卷更新日期:2022-03-04 类型:期中考试
一、单选题
-
1. 实数的相反数是( ).A、2021 B、 C、 D、 .2. 下列运算一定正确的是( )A、 B、 C、 D、3. 芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食物和药物,得到广泛的使用.经测算,一粒芝麻的质量约为 ,将0.00000201用科学记数法表示为( )A、 B、 C、 D、4. 如下摆放的几何体中,主视图与左视图有可能不同的是( )A、
 B、
B、 C、
C、 D、
D、 5. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、6. 某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:
5. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、6. 某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:册数/册
1
2
3
4
5
人数/人
2
5
7
4
2
根据统计表中的数据,这20名同学读书册数的众数,中位数分别是( )
A、3,3 B、3,7 C、2,7 D、7,37. 如图,A,B是双曲线 上的两个点,过点A作AC⊥x轴,交OB于点D,垂足为C,若△ODC的面积为1,D为OB的中点,则k的值为( )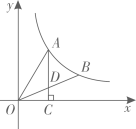 A、 B、2 C、4 D、88. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A、 B、2 C、4 D、88. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )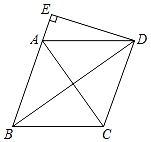 A、 B、 C、4 D、9. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( )
A、 B、 C、4 D、9. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( ) A、57° B、52° C、38° D、26°10. 如图,矩形纸片 中, , .点E、G分别在 , 上,将 、 分别沿 、 翻折,点A的对称点为点F , 点D的对称点为点H , 当E、F、H、C四点在同一直线上时,连接 ,则线段 长为( )
A、57° B、52° C、38° D、26°10. 如图,矩形纸片 中, , .点E、G分别在 , 上,将 、 分别沿 、 翻折,点A的对称点为点F , 点D的对称点为点H , 当E、F、H、C四点在同一直线上时,连接 ,则线段 长为( )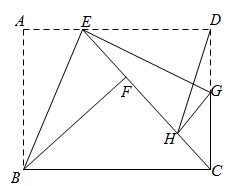 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若二次根式 有意义.则x的取值范围是.12. 分解因式: .13. 在正方形网格中,A , B , C , D , E均为格点,则∠BAC-∠DAE=°.
 14. 已知函数与y轴交于点C,顶点为D.直线交x轴于点E,点F在直线上,且横坐标为4,现在,将抛物线沿其对称轴上下平移,使抛物线与线段总有公共点.抛物线向上最多可以平移个单位长度,向下最多可以平移个单位长度.15. 阅读下面内容,并将问题解决过程补充完整.
14. 已知函数与y轴交于点C,顶点为D.直线交x轴于点E,点F在直线上,且横坐标为4,现在,将抛物线沿其对称轴上下平移,使抛物线与线段总有公共点.抛物线向上最多可以平移个单位长度,向下最多可以平移个单位长度.15. 阅读下面内容,并将问题解决过程补充完整.;
;
……
由此,我们可以解决下面这个问题:
,求出S的整数部分.
解:
……
∴S的整数部分是 .
三、解答题
-
16. 解不等式组:17. 目前,以5G为代表的战略性新兴产业蓬勃发展.某市2019年底有5G用户2万户,计划到2021年底5G用户数累计达到8.72万户.求这两年全市5G用户数的年平均增长率.18. 如图,在平面直角坐标系中,已知点 和 , 请按下列要求画图并填空.
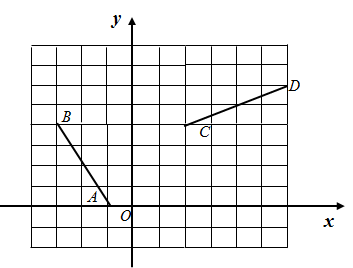
( 1 )沿水平方向移动线段 , 使点A和点C的横坐标相同,画出平移后所得的线段 , 并写出点 的坐标;
( 2 )将线段 绕着某一点旋转一定角度,使其与线段 重合(点 与点C重合,点 与点D重合),请用无刻度的直尺和圆规,找出旋转中心点P.(保留作图痕迹,不写作法)
19. 位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40, ≈1.41).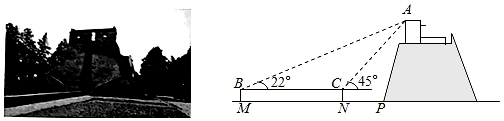 20. 如图,点B为 外一点,过点B作 的切线,切点为A . 点P为 上一点,连接 并延长交 于点C , 连接 ,若 .
20. 如图,点B为 外一点,过点B作 的切线,切点为A . 点P为 上一点,连接 并延长交 于点C , 连接 ,若 .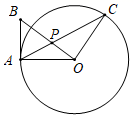 (1)、求证: ;(2)、若 , 的半径为8.求 的长.21. 某学校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数分布直方图.部分信息如下:
(1)、求证: ;(2)、若 , 的半径为8.求 的长.21. 某学校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数分布直方图.部分信息如下: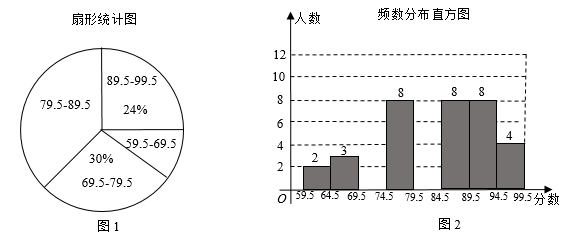 (1)、本次比赛参赛选手共有人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为;(2)、补全图2频数分布直方图;(3)、成绩前四名是2名男生和2名女生,若从他们中任选2人作为该校文艺晚会的主持人,请用列举法(画树状图或列表)求所选取的这两名学生恰好是一男一女的概率.22. 某商店经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
(1)、本次比赛参赛选手共有人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为;(2)、补全图2频数分布直方图;(3)、成绩前四名是2名男生和2名女生,若从他们中任选2人作为该校文艺晚会的主持人,请用列举法(画树状图或列表)求所选取的这两名学生恰好是一男一女的概率.22. 某商店经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)、求出y与x的函数关系式;(2)、问销售该商品第几天时,当天销售利润最大,最大利润是多少?23. 如图,在正方形 中,E , F分别是 , 上的点,且 ,连接 、 、 ,点G是 的中点,连接 并延长交 于点K .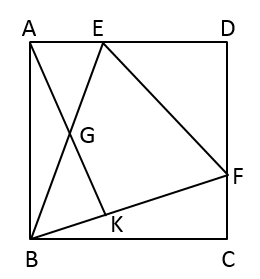 (1)、求证: ;(2)、当点E是 的中点时,求 的值;(3)、连接 ,当线段 取最小值时,求 的值.
(1)、求证: ;(2)、当点E是 的中点时,求 的值;(3)、连接 ,当线段 取最小值时,求 的值.