湘教版初中数学八年级下册第一单元直角三角形单元测试
试卷更新日期:2022-03-04 类型:单元试卷
一、单选题
-
1. 到三角形三边距离相等的点是( )A、三边垂直平分线的交点 B、三条高所在直线的交点 C、三条角平分线的交点 D、三条中线的交点2. 在中, , 如果 , , 那么的长是( ).A、10 B、 C、10或 D、73. 如图.AB=AC,BD=1,BD⊥AD,则数轴上点C所表示的数为( )
 A、 +1 B、- -1 C、- +1 D、 -14. 如图,CD是等腰三角形 △ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,则 △ BCE的面积是( )
A、 +1 B、- -1 C、- +1 D、 -14. 如图,CD是等腰三角形 △ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,则 △ BCE的面积是( ) A、4 B、6 C、8 D、125. 如图,以 的三边为直角边分别向外作等腰直角三角形.若 ,则图中阴影部分的面积为( )
A、4 B、6 C、8 D、125. 如图,以 的三边为直角边分别向外作等腰直角三角形.若 ,则图中阴影部分的面积为( )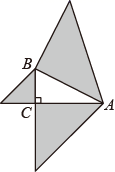 A、3 B、 C、 D、6. 在 中, , , .下列关于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③a是8的算术平方根;④ .其中,所有正确的说法的序号是( )A、①②④ B、②③④ C、①②③ D、①③④7. 下列语句中是命题的有( )
A、3 B、 C、 D、6. 在 中, , , .下列关于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③a是8的算术平方根;④ .其中,所有正确的说法的序号是( )A、①②④ B、②③④ C、①②③ D、①③④7. 下列语句中是命题的有( )①线段垂直平分线上的点到线段两端的距离相等;②作点A关于直线l的对称点A'; ③三边对应相等的两个三角形全等吗?④角平分线上的点到角两边的距离相等.
A、1个 B、2个 C、3个 D、4个8. 如图,在Rt△ABC中,∠ACB是直角,点D是AB边上的中点,下列成立的有( )①∠A+∠B=90° ②AC2+BC2=AB2 ③2CD=AB ④∠B= 30°
 A、①②④ B、①③ C、②④ D、①②③9. 已知等边△ABC的边长为12, D是边AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )A、3 B、4 C、8 D、910. 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为( )
A、①②④ B、①③ C、②④ D、①②③9. 已知等边△ABC的边长为12, D是边AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )A、3 B、4 C、8 D、910. 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为( ) A、44 B、43 C、42 D、4111. 下列命题是真命题的是( )A、同旁内角互补 B、任意一个等腰三角形一定是钝角三角形 C、两边及一角对应相等的两个三角形全等 D、角平分线上的点到角两边的距离相等12. 如图,长方形OABC中,点A在y轴上,点C在x轴上. , . 点D在边AB上,点E在边OC上,将长方形沿直线DE折叠,使点B与点O重合.则点D的坐标为( )
A、44 B、43 C、42 D、4111. 下列命题是真命题的是( )A、同旁内角互补 B、任意一个等腰三角形一定是钝角三角形 C、两边及一角对应相等的两个三角形全等 D、角平分线上的点到角两边的距离相等12. 如图,长方形OABC中,点A在y轴上,点C在x轴上. , . 点D在边AB上,点E在边OC上,将长方形沿直线DE折叠,使点B与点O重合.则点D的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 直角三角形的两条边长分别为3cm、4cm,则这个直角三角形的斜边长为cm.14. 如图,已知Rt△ABC,∠C=90°,BD是角平分线,BD=5,BC=4,则D点到AB的距离是。
 15. 如图,在 中, , 平分 , ,点D到 的距离为5.6,则 .
15. 如图,在 中, , 平分 , ,点D到 的距离为5.6,则 . 16. 如图,等腰△BAC中,∠BAC=120°,BC=6,P为射线BA上的动点,M为BC上一动点,则PM+CP的最小值为 .
16. 如图,等腰△BAC中,∠BAC=120°,BC=6,P为射线BA上的动点,M为BC上一动点,则PM+CP的最小值为 . 17. 如图,Rt△ABC中,∠A=90°,AB=3,AC=4,现将△ABC沿BD进行翻折,使点A刚好落在BC上,则CD=.
17. 如图,Rt△ABC中,∠A=90°,AB=3,AC=4,现将△ABC沿BD进行翻折,使点A刚好落在BC上,则CD=. 18. 如图,△ABC中,AB=AC=13,BC=24,点D在BC上(BD>CD),△AED与△ACD关于直线AD轴对称,点C的对称点是点E,AE交BC于点F,连结BE,CE.当DE⊥BC时,∠ADE的度数为 , CE的长为 .
18. 如图,△ABC中,AB=AC=13,BC=24,点D在BC上(BD>CD),△AED与△ACD关于直线AD轴对称,点C的对称点是点E,AE交BC于点F,连结BE,CE.当DE⊥BC时,∠ADE的度数为 , CE的长为 . 19. 如图,在△ABC中,∠ACB=90°,∠A=30°,边AC的垂直平分线DE分别交边AB、AC于点D、E、P为直线DE上一点.若BC=2,则△BCP周长的最小值为 .
19. 如图,在△ABC中,∠ACB=90°,∠A=30°,边AC的垂直平分线DE分别交边AB、AC于点D、E、P为直线DE上一点.若BC=2,则△BCP周长的最小值为 .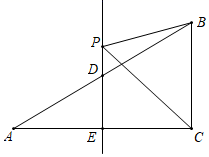 20. 如图,是的角平分线, , , , 则的长为 .
20. 如图,是的角平分线, , , , 则的长为 . 21. 小明学了在数轴上表示无理数的方法后,进行了练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=1;再以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,那么点P表示的数是 .
21. 小明学了在数轴上表示无理数的方法后,进行了练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=1;再以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,那么点P表示的数是 . 22. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是
22. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是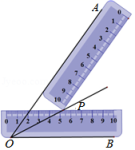
三、作图题
-
23. 作图题:(保留作图痕迹,不必写作法)
如图,已知△ABC中,AB=2AC,作一条射线AD交线段BC于点D,使△ABD的面积是△ACD的面积的2倍.
 24. 如图,已知线段 , .
24. 如图,已知线段 , . (1)、尺规作图:作等腰 , 使底边长为 , 上的高为.(2)、若 , , 求的周长.
(1)、尺规作图:作等腰 , 使底边长为 , 上的高为.(2)、若 , , 求的周长.四、解答题
-
25. 如图,在 中,D为 的中点, , ,垂足分别为E,F,且 , ,求证: 是等边三角形.
 26. 滑撑杆在悬窗中应用广泛.如图,某款滑撑杆由滑道 ,撑杆 、 组成,滑道 固定在窗台上.悬窗关闭或打开过程中,撑杆 、 的长度始终保持不变.当悬窗关闭时,如图①,此时点A与点O重合,撑杆 、 恰与滑道 完全重合;当悬窗完全打开时,如图②,此时撑杆 与撑杆 恰成直角,即 ,测量得 ,撑杆 ,求滑道 的长度.
26. 滑撑杆在悬窗中应用广泛.如图,某款滑撑杆由滑道 ,撑杆 、 组成,滑道 固定在窗台上.悬窗关闭或打开过程中,撑杆 、 的长度始终保持不变.当悬窗关闭时,如图①,此时点A与点O重合,撑杆 、 恰与滑道 完全重合;当悬窗完全打开时,如图②,此时撑杆 与撑杆 恰成直角,即 ,测量得 ,撑杆 ,求滑道 的长度. 27. 如图,△ABC中,∠ABC=45°,F是高AD和高BE的交点,AC= , BD=2.求线段DF的长度.
27. 如图,△ABC中,∠ABC=45°,F是高AD和高BE的交点,AC= , BD=2.求线段DF的长度.
五、综合题
-
28. 如图,在 中, , ,F为 延长线上一点,点E在 上,且 .
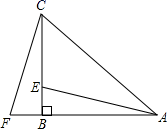 (1)、求证: ;(2)、若 ,求 的度数.29. 如图所示, 中, , 于点 , , .
(1)、求证: ;(2)、若 ,求 的度数.29. 如图所示, 中, , 于点 , , .
 (1)、求 , 的长.(2)、若点 是射线 上的一个动点,作 于点 ,连结 .
(1)、求 , 的长.(2)、若点 是射线 上的一个动点,作 于点 ,连结 .①当点 在线段 上时,若 是以 为腰的等腰三角形,请求出所有符合条件的 的长.
②设 交直线 于点 ,连结 , ,若 ,则 的长为多少?(直接写出结果).
30. (1)、阅读理解:问题:如图1,在四边形 中,对角线 平分 , .求证: .
(1)、阅读理解:问题:如图1,在四边形 中,对角线 平分 , .求证: .思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在 上截取 ,连接 ,得到全等三角形,进而解决问题;
方法2:延长 到点N,使得 ,连接 ,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种 , 添加辅助线并完成证明.
(2)、问题解决:如图2,在(1)的条件下,连接 ,当 时,探究线段 , , 之间的数量关系,并说明理由;(3)、问题拓展:如图3,在四边形 中, , ,过点D作 ,垂足为点E,请直接写出线段 、 、 之间的数量关系.