2021-2022学年度第二学期七年级数学第五章《相交线与平行线》5.3平行线的性质课堂练习卷
试卷更新日期：2022-03-04 类型：同步测试
一、单选题
-
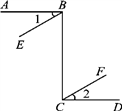
1. 如图，AD∥BC，∠C＝30°，∠ADB：∠BDC＝1：2，∠EAB＝72°，以下四个说法：
①∠CDF＝30°；②∠ADB＝50°；
③∠ABD＝22°；④∠CBN＝108°
其中正确说法的个数是（ ）
A、1个 B、2个 C、3个 D、4个2. 如图，AB∥CD，AE∥CF，∠A=41°，则∠C的度数为（ ）
A、139° B、141° C、131° D、129°3. 如图，直线AB∥CD，直线AB、CD被直线EF所截，交点分别为点M、点N，若∠AME＝130°，则∠DNM的度数为（ ）
A、30° B、40° C、50° D、60°4. 如图，直尺的一条边经过直角三角尺的直角顶点且平分直角，它的对边恰巧经过60°角的顶点．则∠1的大小是（ ）
A、30° B、45° C、60° D、75°5. 如图，已知AD//BC，∠B=32°，DB平分∠ADE，则∠DEC=（ ）
A、64° B、66° C、74° D、86°6. 下列选项中，可以用来证明命题“若a>b，则|a|>|b|”是假命题的反例是（ ）A、a=1，b=0 B、u=-1，b=2 C、a=-2，b=1 D、a=1，b=-37. 能说明命题“对于任意实数a，都有a2＞0”是假命题的反例是（ ）A、a＝﹣2 B、a＝1 C、a＝0 D、a＝8. 下列说法不正确的是（ ）A、任意一个直角三角形都可以被分割成两个等腰三角形 B、任意一个等腰三角形都可以被分割成两个等腰三角形 C、任意一个直角三角形都可以被分割成两个直角三角形 D、任意一个等腰三角形都可以被分割成两个直角三角形9. 下列说法中，错误的是（ ）A、对顶角相等 B、三角形内角和等于180° C、三角形的一个外角大于任何一个内角 D、两直线平行，同旁内角互补10. 下列结论中，正确的是（ ）A、过任意三点一定能画一条直线 B、两点之间线段最短 C、射线AB和射线BA是同一条射线 D、经过一点的直线只有一条二、填空题
-
11. 一艘旅游船从 点出发沿北偏东 方向航行，到达 景点后，进行了 的转弯，然后沿着 方向航行，则 为方向．12. 如图， ， 平分 ， ， 则 ．
13. 如图，AB∥CD∥EF，若∠ABC＝125°，∠CEF＝105°，则∠BCE的度数为 ．
14. 若要证明命题“若a2>1，则a>1”是假命题，则可以举一个反例是。15. 命题“a＜2a”是 命题（填“真”或“假”）.三、解答题
-
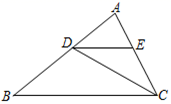
16. 如图，已知DE∥BC，BE是∠ABC的平分线，∠C=70°，∠ABC=50°．求∠DEB和∠BEC的度数．
17. 根据解答过程填空（写出推理理由或数学式）：如图，已知∠DAF＝∠F，∠B＝∠D，试说明AB∥DC．
证明：∵∠DAF＝∠F（已知）．
∴AD∥BF（ ▲ ），
∴∠D＝∠DCF（ ▲ ）．
∵∠B＝∠D（已知），
∴（ ▲ ）＝∠DCF（等量代换），
∴AB∥DC（ ▲ ）．
18. 如图，如果∠1＝60°，∠2＝120°，∠D＝60°，那么AB与CD平行吗？BC与DE呢？
观察下面的解答过程，补充必要的依据或结论．
解∵∠1＝60°（已知）
∠ABC＝∠1 （① ▲ ）
∴∠ABC＝60°（等量代换）
又∵∠2＝120°（已知）
∴（② ▲ ）+∠2＝180°（等式的性质）
∴AB∥CD （③ ▲ ）
又∵∠2+∠BCD＝（④ ▲ °）
∴∠BCD＝60°（等式的性质）
∵∠D＝60°（已知）
∴∠BCD＝∠D （⑤ ▲ ）
∴BC∥DE （⑥ ▲ ）
19. 如图，已知AB∥DE，∠1=18°，∠2=125°，求∠BCD的度数．
