2022年初中数学浙教版七年级下册3.5整式的化简能力阶梯训练——普通版

试卷更新日期：2022-03-04 类型：同步测试

进入出卷网下载

一、单选题

1. 计算（x+3y）²-（3x+y）²的结果是（）

A、8x²-8y² B、8y²-8x² C、8（x+y）² D、8（x-y）²

查看试题解析
2. 如果x²+x=3，那么代数式（x+1）（x-1）+x（x+2）的值是（）

A、2 B、3 C、5 D、6

查看试题解析
3. 当x=- $\frac{7}{12}$ 时，代数式（x-2）²-2（2-2x）-（1+x）（1-x）的值等于（）

A、- $\frac{23}{72}$ B、 $\frac{23}{72}$ C、1 D、 $\frac{49}{72}$

查看试题解析
4. 当x=3，y=1时，代数式（x+y）（x-y）+y²的值是（）

A、6 B、8 C、9 D、12

查看试题解析
5. 已知 $M = 2022^{2} ， N = 2021 \times 2023$ ，则 $M$ 与 $N$ 的大小关系是（）

A、 $M > N$ B、 $M < N$ C、 $M = N$ D、不能确定

查看试题解析

二、填空题

6. 已知 $m + n = 12$ ， $m - n = 2$ ，则 $m^{2} - n^{2} =$ .

查看试题解析
7. 若 $a x^{2} + 2 x + \frac{1}{2} = {(2 x + \frac{1}{2})}^{2} + m$ ，则 $a$ ， $m$ 的值分别是．

查看试题解析
8. 计算 $2021^{2} - 2019 \times 2023$ 的结果是.

查看试题解析
9. 若 $a$ ， $b$ 互为相反数，则 $a^{2} - b^{2} =$ .

查看试题解析
10. 设某个长方形的长和宽分别为 $a$ 和 $b$ ，周长为14，面积为10，则 ${(a + b)}^{2} =$ ， $a^{2} + b^{2} =$ ．

查看试题解析

三、综合题

11.

(1)、先化简，再求值：6x²y（﹣2xy+y³）÷xy² ，其中x＝2，y＝﹣1；

(2)、已知 $a - b = 7$ ， $a b = - 12$ ．分别求 $a^{2} + b^{2}$ ， $a + b$ 的值；

查看试题解析
12. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1可以得到 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ ，请解答下列问题：

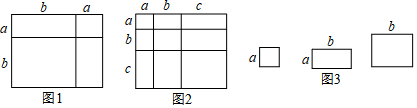(1)、写出图2中所表示的数学等式.

(2)、利用（1）中得到的结论，解决下面的问题：若 $a + b + c = 8 ， a^{2} + b^{2} + c^{2} = 36$ ，求 $a b + b c + a c$ 的值.

(3)、小明同学用图 $3$ 中 $x$ 张边长为 $a$ 的正方形， $y$ 张边长为 $b$ 的正方形 $z$ 张边长分别为 $a ， b$ 的长方形纸片拼出一个面积为 $(4 a + 7 b) (6 a + 5 b)$ 长方形，求 $x + y + z$ 的值.

查看试题解析
13. （知识回顾）
七年级学习代数式求值时，遇到这样一类题“代数式 $a x - y + 6 + 3 x - 5 y - 1$ 的值与x的取值无关，求a的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含x项的系数为0，即原式= $(a + 3) x - 6 y + 5$ ，所以 $a + 3 = 0$ ，则 $a = - 3$ .

(1)、（理解应用）
若关于x的多项式 $(2 x - 3) m + 2 m^{2} - 3 x$ 的值与x的取值无关，求m值；

(2)、已知 $A = (2 x + 1) (x - 1) - x (1 - 3 y)$ ， $B = - x^{2} + x y - 1$ ，且3A+6B的值与x无关，求y的值；

(3)、（能力提升）
7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分(图中阴影部分)，设右上角的面积为 $S_{1}$ ，左下角的面积为 $S_{2}$ ，当AB的长变化时， $S_{1} - S_{2}$ 的值始终保持不变，求a与b的等量关系.

查看试题解析

2022年初中数学浙教版七年级下册3.5整式的化简 能力阶梯训练——普通版

一、单选题

二、填空题

三、综合题

2022年初中数学浙教版七年级下册3.5整式的化简能力阶梯训练——普通版