2022年初中数学浙教版七年级下册3.4乘法公式能力阶梯训练——普通版

试卷更新日期：2022-03-04 类型：同步测试

进入出卷网下载

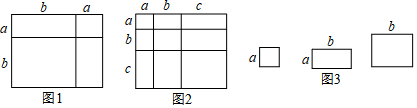
1. 下列不能用平方差公式运算的是（）

A、 $(x + 1) (x - 1)$ B、 $(- x + 1) (- x - 1)$ C、 $(x + 1) (- x + 1)$ D、 $(x + 1) (1 + x)$

查看试题解析
2. 已知 $(a - b)^{2} = 6 ， (a + b)^{2} = 4$ ，则 $a^{2} + b^{2}$ 的值（）

A、10 B、6 C、5 D、3

查看试题解析
3. 已知x，y满足 ${\begin{matrix} x + 3 y = - 1 \\ x - 3 y = 5 \end{matrix}$ ，则 $x^{2} - 9 y^{2}$ 的值为（）

A、-5 B、4 C、5 D、25

查看试题解析
4. 图（1）是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（）

A、 ${(a - b)}^{2}$ B、 ${(a + b)}^{2}$ C、ab D、a²－b²

查看试题解析
5. 化简 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) (2^{16} + 1)$ 的结果是（）

A、 $2^{32} - 1$ B、 $2^{32} + 1$ C、 ${(^{} + 1)}^{2}$ D、 ${(^{} - 1)}^{2}$

查看试题解析

6. 设 $x$ 表示 $\sqrt{5}$ 的整数部分， $y$ 表示它的小数部分，求 $(\sqrt{5} + x) y =$ .

查看试题解析
7. 若9x²-2（m－4）x＋16是一个完全平方式，则m的值为．

查看试题解析
8. 已知 $x - \frac{1}{x} = 7$ ，则 $x^{2} + \frac{1}{x^{2}} =$ ．

查看试题解析
9. 若 ${(x + y)}^{2} = 10$ ， $x y = 2$ ，则 $x^{2} + y^{2} =$ .

查看试题解析
10. 如图，将大正方形通过剪、割、拼后分解成新的图形，利用等面积法可证明某些乘法公式，在给出的4幅拼法中，其中能够验证平方差公式的有（填序号，多选）.

查看试题解析

2022年初中数学浙教版七年级下册3.4乘法公式 能力阶梯训练——普通版