浙江省宁波市鄞州区2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-03-02 类型：期末考试

进入出卷网下载

一、单选题

1. 如果 $x ： y = 2 ： 3$ ，那么 $\frac{x}{x + y}$ 的值是（）

A、 $\frac{2}{5}$ B、 $\frac{5}{2}$ C、 $\frac{3}{5}$ D、 $\frac{5}{3}$

查看试题解析
2. 下列事件是必然事件的是（）

A、抛一枚骰子朝上数字是6 B、打开电视正在播放疫情相关新闻 C、煮熟的鸡蛋稃出一只小鸡 D、400名学生中至少有两人生日同一天

查看试题解析
3. 下列二次函数的图象中，顶点在第二象限的是（）

A、 $y = {(x - 1)}^{2} + 3$ B、 $y = {(x - 1)}^{2} - 3$ C、 $y = {(x + 1)}^{2} + 3$ D、 $y = {(x + 1)}^{2} - 3$

查看试题解析
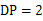4. 如图， $△ A B C$ 中， $A B = A C = 10 cm ， B C = 12 cm ， A D ⊥ B C$ 于点D，点P为 $A D$ 上的点，，以点P为圆心 $6 cm$ 为半径画圆，下列说法错误的是（）

A、点A在 $⊙ P$ 外 B、点B在 $⊙ P$ 外 C、点C在 $⊙ P$ 外 D、点D在 $⊙ P$ 内

查看试题解析
5. 已知 $tan A = 1.5$ ，则 $∠ A$ 的度数所属范围是（）

A、 B、 $45^{\circ} < ∠ A < 60^{\circ}$ C、 $60^{\circ} < ∠ A < 75^{\circ}$ D、 $75^{\circ} < ∠ A < 90^{\circ}$

查看试题解析
6. 直角三角形的外接圆半径为3，内切圆半径为1，则该直角三角形的周长是（）

A、12 B、14 C、16 D、18

查看试题解析
7. 一个球从地面竖直向上弹起时的速度为8米/秒，经过t秒时球的高度为h米，h和t满足公式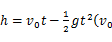：表示球弹起时的速度，g表示重力系数，取 $g = 10$ 米/秒 $^{2})$ ，则球不低于3米的持续时间是（）

A、 $0.4$ 秒 B、 $0.6$ 秒 C、 $0.8$ 秒 D、1秒

查看试题解析
8. 如图， $B D$ 是 $△ A B C$ 的角平分线， $D E ∥ B C$ 交 $A B$ 于点E，若 $△ A B C$ 的重心G在 $D E$ 上，则 $A B ： B C$ 的值是（）

A、 $3 ： 2$ B、 $7 ： 4$ C、 $2 ： 1$ D、 $8 ： 5$

查看试题解析
9. 二次函数 $y = a x^{2} + (1 - a) x + 4 - 2 a$ 的图象如图所示，则下列说法正确的是（）

A、与y轴交点的纵坐标小于4 B、对称轴在直线 $x = 0.5$ 左侧 C、与x轴正半轴交点的横坐标小于2 D、拋物线一定经过两个定点

查看试题解析
10. 如图， $⊙ O$ 是锐角 $△ A B C$ 的外接圆，直径 $A D$ 平分 $∠ B A C$ 交 $B C$ 于于F， $E G ⊥ A C$ 于G，连结 $D F ， D G$ ，要求四边形 $A F D G$ 面积，只需知道下列选项中某个三角形的面积，则这个三角形是（）

A、 $△ A E G$ B、 $△ B E F$ C、 $△ A B C$ D、 $△ D E G$

查看试题解析

二、填空题

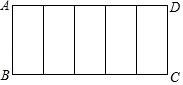
11. 一个圆内接正多边形的一条边所对的圆心角是60°，则该正多边形边数是.

查看试题解析
12. 某视听节目从200名打通热线电话的听众中抽取10名“幸运听众”，则打通一次热线电话的听众成为 “幸运听众”的概率是.

查看试题解析
13. 如图，矩形 $A B C D$ 被分割为5个全等的长方形，若这5个矩形都与矩形 $A B C D$ 相似，则 $A D ： A B$ 的值是.

查看试题解析
14. 如图，一架梯子斜靠在墙上，梯子底端到墙的距离BC为4米， $cos ∠ A B C = \frac{3}{4}$ ，则梯子 $A B$ 的长是米.

查看试题解析
15. 如图，平面直角坐标系中有一点 $A (4 ， 2)$ ，在以 $M (0 ， 3)$ 为圆心，2为半径的圆上有一点P，将点P绕点A旋转 $180^{\circ}$ 后恰好落在x轴上，则点P的坐标是.

查看试题解析
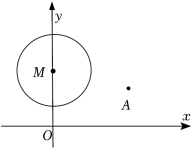16. 如图，点A是抛物线 $y = \frac{1}{8} x^{2}$ 上不与原点O重合的动点. $A B ⊥ x$ 轴于点B，过点B作 $O A$ 的垂线并延长交y轴于点C，连结 $A C$ ，则线段 $O C$ 的长是， AC的最小值是.

查看试题解析

三、解答题

17.

(1)、计算： $cos 30^{\circ} \cdot tan 60^{\circ} - {sin}^{2} 45^{\circ}$ ；

(2)、已知实数x满足 $x ： 3 = (x + 2) ： 4$ ，求x的值.

查看试题解析
18. 一个不透明口袋里装有4个除颜色外其他完全相同的球，其中红球2个，黄球1个，白球1个.

(1)、从中任取一个球，求摸到红球的概率；

(2)、若第一次从口袋中任意摸出1个球，不放回，第二次再摸出1个球.用列表或画树状图写出所有可能性，并求出刚好摸到一个红球和一个白球的概率.

查看试题解析
19. 如图，由边长为1的小正方形组成的 $6 \times 6$ 网格中， $△ A B C$ 顶点在网格上，点D在 $B C$ 边上，且 $B D = 2 C D$ .

(1)、 $B D$ 长等于.

(2)、请你仅用无刻度的直尺在边 $A B$ 上找点E，使得 $△ B D E$ 与 $△ A B C$ 相似.（要求画出两种情形）

查看试题解析
20. 如图，某渔船向正东方向以14海里/时的速度航行，在A处测得小岛C在北偏东 $70^{\circ}$ 方向，2小时后渔船到达B处，测得小岛C在北偏东 $45^{\circ}$ 方向，已知该岛周围20海里范围内有暗礁.（参考数据： $sin 70^{\circ} \approx 0.94 ， cos 70^{\circ} \approx 0.34 ， tan 70^{\circ} \approx 2.75 ， \sqrt{2} \approx 1.41$ ）

(1)、求B处距离小岛C的距离（精确到 $0.1$ 海里）；

(2)、为安全起见，渔船在B处向东偏南转了 $25^{\circ}$ 继续航行，通过计算说明船是否安全？

查看试题解析
21. 如图， $A B$ 是 $⊙ O$ 的直径， $C ， D$ 是圆上两点，且有 $\overset{⌢}{BD} = \overset{⌢}{C D}$ ，连结 $A D ， A C$ ，作 $D E ⊥ A C$ 的延长线于点E.

(1)、求证： $D E$ 是 $⊙ O$ 的切线；

(2)、若 $A D = 2 \sqrt{3} ， ∠ A D E = 60^{\circ}$ ，求阴影部分的面积.（结果保留 $π$ ）

查看试题解析
22. 如图，抛物线 $y = \frac{1}{2} x^{2} + 2 x + c$ 经过点 $A (0 ， 3)$ ，将该抛物线平移后，点 $A (0 ， 3)$ 到达点 $B (4 ， 1)$ 的位置.

(1)、求平移后抛物线的解析式，并在同一平面直角坐标系中画出平移后的抛物线；

(2)、过点B画平行于y轴的直线交原抛物线于点C，求线段 $B C$ 的长；

(3)、若平行于y轴的直线 $l ： x = m$ 与两条抛物线的交点是 $P ， Q$ ，当线段 $P Q$ 的长度超过6时，求m的取值范围.

查看试题解析
23. 如图1， $△ A B C$ 是等边三角形，D是 $A C$ 边上不与点A重合的一点，延长 $B C$ 到点E，使得 $C E = A D$ ，延长 $A C$ 到F使 $C F = A C$ ，连结 $E F ， B D$ .

(1)、若 $∠ A B D = 20^{\circ}$ ，求 $∠ C F E$ 和 $∠ C E F$ 的度数.

(2)、如图2，取 $B D$ 的中点M，连结 $A M ， A E$ ，求证： $A E = 2 A M$ .

(3)、在（2）的条件下，连结 $E M$ ，判断 $A M$ 和 $E M$ 的位置关系和数量关系并说明理由.

查看试题解析
24. 【问题提出】如图1， $△ A B C$ 中，线段 $D E$ 的端点 $D ， E$ 分别在边 $A B$ 和 $A C$ 上，若位于 $D E$ 上方的两条线段 $A D$ 和 $A E$ 之积等于 $D E$ 下方的两条线段 $B D$ 和 $C E$ 之积，即 $A D \times A E = B D \times C E$ ，则称 $D E$ 是 $△ A B C$ 的“友好分割”线段.

(1)、如图1，若 $D E$ 是 $△ A B C$ 的“友好分割”线段，，求 $A C$ 的长；

(2)、【发现证明】如图2， $△ A B C$ 中，点F在 $B C$ 边上， $F D ∥ A C$ 交 $A B$ 于D， $F E ∥ A B$ 交 $A C$ 于E，连结 $D E$ ，求证： $D E$ 是 $△ A B C$ 的“友好分割”线段；

(3)、【综合运用】如图3， $D E$ 是 $△ A B C$ 的“友好分割”线段，连结 $D E$ 并延长交 $B C$ 的延长线于F，过点A 画 $A G ∥ D E$ 交 $△ A D E$ 的外接圆于点G，连结 $G E$ ，设 $\frac{A D}{D B} = x ， \frac{F C}{F B} = y$ .
①求y关于x的函数表达式；

②连结 $B G ， C G$ ，当 $y = \frac{9}{16}$ 时，求 $\frac{B G}{C G}$ 的值.

查看试题解析