贵州省毕节市2021-2022学年九年级上学期期末数学试卷
试卷更新日期:2022-03-02 类型:期末考试
一、单选题
-
1. 将一元二次方程 化为一般形式后,其中二次项系数、一次项系数、常数项分别是( )A、 B、 C、 D、2. 如图所示的几何体,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列各组线段中是成比例线段的是( )A、 B、 C、 D、4. 下列方程中,没有实数根的是( )A、 B、 C、 D、5. 如图,在 中, ,则 的长为( )
3. 下列各组线段中是成比例线段的是( )A、 B、 C、 D、4. 下列方程中,没有实数根的是( )A、 B、 C、 D、5. 如图,在 中, ,则 的长为( ) A、4 B、6 C、8 D、106. 有4张背面相同的卡片,正面分别印有平行四边形、矩形、菱形、正方形,现将4张卡片正面朝下一字摆开,从中随机抽取两张,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为( )A、1 B、 C、 D、7. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、8. 如图,在 中,点 分别在 边上, 与 不平行,那么下列条件中,不能判定 的是( )
A、4 B、6 C、8 D、106. 有4张背面相同的卡片,正面分别印有平行四边形、矩形、菱形、正方形,现将4张卡片正面朝下一字摆开,从中随机抽取两张,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为( )A、1 B、 C、 D、7. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、8. 如图,在 中,点 分别在 边上, 与 不平行,那么下列条件中,不能判定 的是( )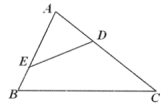 A、 B、 C、 D、9. 若 是关于x的一元二次方程 的一个根,则 的值为( )A、2018 B、2020 C、2022 D、202410. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,DB=8,AE⊥BC于点E,则AE=( )
A、 B、 C、 D、9. 若 是关于x的一元二次方程 的一个根,则 的值为( )A、2018 B、2020 C、2022 D、202410. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,DB=8,AE⊥BC于点E,则AE=( ) A、6 B、8 C、 D、11. “双减”期间,某校音乐社团购买了一种乐器,如图.乐器上的一根弦 ,两个端点 固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则 之间的距离为( )
A、6 B、8 C、 D、11. “双减”期间,某校音乐社团购买了一种乐器,如图.乐器上的一根弦 ,两个端点 固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则 之间的距离为( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,已知点 ,以原点O为位似中心,相似比为 ,把 缩小,则点A的对应点 的坐标是( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,已知点 ,以原点O为位似中心,相似比为 ,把 缩小,则点A的对应点 的坐标是( )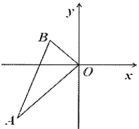 A、 B、 或 C、 D、 或13. 如图,O是矩形 的对角线 的中点,E是 边的中点.若 ,则线段 的长为( )
A、 B、 或 C、 D、 或13. 如图,O是矩形 的对角线 的中点,E是 边的中点.若 ,则线段 的长为( )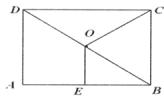 A、3 B、4 C、5 D、614. 已知 是关于x的一元二次方程 的两个不相等的实数根,且满足 ,则m的值为( )A、 或1 B、 或3 C、 D、315. 如图,在直角坐标系中,点 是一个光源.木杆 两端的坐标分别为 .则木杆 在x轴上的投影长为( )
A、3 B、4 C、5 D、614. 已知 是关于x的一元二次方程 的两个不相等的实数根,且满足 ,则m的值为( )A、 或1 B、 或3 C、 D、315. 如图,在直角坐标系中,点 是一个光源.木杆 两端的坐标分别为 .则木杆 在x轴上的投影长为( ) A、8 B、9 C、10 D、12
A、8 B、9 C、10 D、12二、填空题
-
16. 已知关于x的一元二次方程(a﹣3)x2+2x+a2﹣9=0的一个根是0,则a=.17.
如图,在 中, 分别为 的中点.若 ,则 的长度为. 18. 已知a,b,c为非零实数,且 ,则k的值为.19. 如图,正方形ABCD的边长为4,E是BC的中点,在对角线BD上有一点P,则PC+PE的最小值是.
18. 已知a,b,c为非零实数,且 ,则k的值为.19. 如图,正方形ABCD的边长为4,E是BC的中点,在对角线BD上有一点P,则PC+PE的最小值是.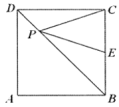 20. 如图,点 是反比例函数 图象上的两点,过点 分别作 轴于点 轴于点B,连接 ,已知点 ,则 .
20. 如图,点 是反比例函数 图象上的两点,过点 分别作 轴于点 轴于点B,连接 ,已知点 ,则 .
三、解答题
-
21. 解方程(1)、(2)、22. 小明想利用阳光下的影长测量学校旗杆 的高度.如图,他在某一时刻在地面上竖直立一个2米长的标杆 ,测得其影长 米.
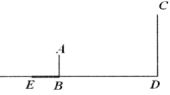 (1)、请在图中画出此时旗杆 在阳光下的投影 .(2)、如果 米,求旗杆 的高.23. 某校为了贯彻“减负增效”精神,掌握九年级800名学生每天的自主学习情况,该校领导随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)、请在图中画出此时旗杆 在阳光下的投影 .(2)、如果 米,求旗杆 的高.23. 某校为了贯彻“减负增效”精神,掌握九年级800名学生每天的自主学习情况,该校领导随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题: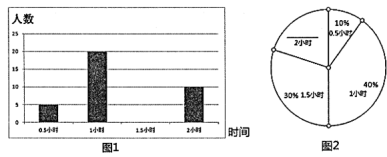 (1)、本次调查的学生人数是人;(2)、将条形统计图图1和扇形统计图图2补充完整;(3)、请估算,该校九年级自主学习时间不少于1.5小时的学生有人;(4)、老师想从学习效果较好的3位同学(分别记为 ,其中B为小华)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小华B的概率.24. 如图, 中, 分别是 的中点, ,过点B作 ,交 的延长线于点F.
(1)、本次调查的学生人数是人;(2)、将条形统计图图1和扇形统计图图2补充完整;(3)、请估算,该校九年级自主学习时间不少于1.5小时的学生有人;(4)、老师想从学习效果较好的3位同学(分别记为 ,其中B为小华)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小华B的概率.24. 如图, 中, 分别是 的中点, ,过点B作 ,交 的延长线于点F. (1)、求证:四边形 是菱形.(2)、若 ,求菱形 的面积.25. 毕节市大方县某口罩厂今年7月份的生产成本是1000万元,由于改进技术,生产成本逐月下降,9月份的生产成本是810万元.假设该公司 月每个月生产成本的下降率都相同.(1)、求每个月生产成本的下降率;(2)、若月平均下降率不变,请求10月份该公司的生产成本.
(1)、求证:四边形 是菱形.(2)、若 ,求菱形 的面积.25. 毕节市大方县某口罩厂今年7月份的生产成本是1000万元,由于改进技术,生产成本逐月下降,9月份的生产成本是810万元.假设该公司 月每个月生产成本的下降率都相同.(1)、求每个月生产成本的下降率;(2)、若月平均下降率不变,请求10月份该公司的生产成本.

