广西壮族自治区百色市2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-03-02 类型：期末考试

进入出卷网下载

一、单选题

1. 二次函数 $y = {(x - 1)}^{2} - 3$ 的最小值是（）

A、2 B、1 C、 $- 2$ D、 $- 3$

查看试题解析
2. $△ A B C$ 中， $∠ A$ ， $∠ B$ 均为锐角，且有 $| \tan B - \sqrt{3} | + {(\sin A - \frac{\sqrt{3}}{2})}^{2} = 0$ ，则 $△ A B C$ 是（）

A、直角（不等腰）三角形 B、等边三角形 C、等腰（不等边）三角形 D、等腰直角三角形

查看试题解析
3. 如图，为了测量河两岸 $A$ 、 $B$ 两点的距离，在与 $A B$ 垂直的方向点 $C$ 处测得 $A C = a$ ， $∠ A C B = α$ ，那么 $A B$ 等于（）

A、 $a \cdot sin α$ B、 $a \cdot tan α$ C、 $a \cdot cos α$ D、 $\frac{a}{tan α}$

查看试题解析
4. 如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，若BD=2AD，则（）

A、 $\frac{A D}{A B} = \frac{1}{2}$ B、 $\frac{A E}{E C} = \frac{1}{2}$ C、 $\frac{A D}{E C} = \frac{1}{2}$ D、 $\frac{D E}{B C} = \frac{1}{2}$

查看试题解析
5. 将二次函数y= $\frac{1}{4}$ x²+x﹣1化为y=a（x+h）²+k的形式是（）

A、y= $\frac{1}{4} {(x + 2)}^{2} + 2$ B、y= $\frac{1}{4}$ （x﹣2）²﹣2 C、y= $\frac{1}{4}$ （x+2）²﹣2 D、y= $\frac{1}{4}$ （x﹣2）²+2

查看试题解析
6. 若A（a₁ ， b₁），B（a₂ ， b₂）是反比例函数y= $\frac{1}{x}$ （x＞0）图象上的两个点，且a₁＜a₂ ，则b₁与b₂的大小关系是（　　）

A、b₁＞b₂ B、b₁=b₂ C、b₁＜b₂ D、大小不确定

查看试题解析
7. 如图，某水库堤坝横断面迎水坡AB的斜面坡度是1： $\sqrt{3}$ ，堤坝高BC=50m，则迎水坡面AB的长度是（）

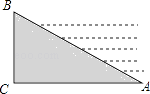A、100m B、120m C、50 $\sqrt{3}$ m D、100 $\sqrt{3}$ m

查看试题解析
8. 如图，A，B是反比例函数 $y = \frac{8}{x}$ 图象上的两点，分别过点A，B作x轴，y轴的垂线，构成图中的三个相邻且不重叠的小矩形 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ，已知 $S_{2} = 3$ ， $S_{1} + S_{3}$ 的值为（）

A、16 B、10 C、8 D、5

查看试题解析
9. 小明身高1.5米，在操场的影长为2米，同时测得教学大楼在操场的影长为60米，则教学大楼的高度应为（）

A、45米 B、40米 C、90米 D、80米

查看试题解析
10. 如图，在菱形ABCD中， $D E ⊥ A B$ ， $\cos A = \frac{3}{5}$ ， $A E = 6$ ，则AB的长为是（）

A、6 B、8 C、10 D、12

查看试题解析
11.
如图，在△ABC中，AB=24，AC=18，D是AC上一点，AD=12．在AB上取一点E ．使A、D、E三点组成的三角形与△ABC相似，则AE的长为（　　）.

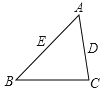A、16 B、14 C、16或14 D、16或9

查看试题解析
12. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴交于点A、B两点，与y轴交于点C；对称轴为直线 $x = - 1$ ，点B的坐标为 $(1 ， 0)$ ，则下列结论：① $A B = 4$ ；② $b^{2} - 4 a c > 0$ ；③ $b > 0$ ；④ $a - b + c < 0$ ，其中正确的结论有（）个.

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 关于x的函数 $y = (m + 2) x^{m^{2} - 2}$ 是二次函数，则m的值是.

查看试题解析
14.
如图，△ABC与△DEF是位似图形，相似比为5：7，已知DE=14，则AB的长为

查看试题解析
15. 如图，四边形ADEF为菱形，且 $A B = 6$ ， $A C = 4$ ，那么 $D E =$ .

查看试题解析
16. 在反比例函数 $y = \frac{1 - k}{x}$ 的图象每一条分支上，y都随x的增大而增大，则k的取值范围是.

查看试题解析
17. α是锐角，若sinα＝cos15°，则α＝°.

查看试题解析
18. 将边长分别为2、3、5的三个正方形按图所示的方式排列，则图中阴影部分的面积为.

查看试题解析

三、解答题

19. 计算：2cos45°﹣tan60°+sin30°﹣|﹣ $\frac{1}{2}$ |．

查看试题解析
20. 如图，一次函数y₁=﹣x﹣1的图象与x轴交于点A，与y轴交于点B，与反比例函数y₂= $\frac{k}{x}$ 图象的一个交点为M（﹣2，m）.

(1)、求反比例函数的解析式；

(2)、求△MOB的面积.

查看试题解析
21. 已知， $△ D E F$ 是 $△ A B C$ 的位似三角形（点D、E、F分别对应点A、B、C），原点O为位似中心， $△ D E F$ 与 $△ A B C$ 的位似比为k.

(1)、若位似比 $k = \frac{1}{2}$ ，请你在平面直角坐标系的第四象限中画出 $△ D E F$ ；

(2)、若位似比 $k = n$ ， $△ A B C$ 的面积为S，则 $△ D E F$ 的面积＝.

查看试题解析
22. 某高中学校为高一新生设计的学生板凳的正面视图如图所示，其中BA=CD，BC=20cm，BC、EF平行于地面AD且到地面AD的距离分别为40cm、8cm.为使板凳两腿底端A、D之间的距离为50cm，那么横梁EF应为多长？（材质及其厚度等暂忽略不计）.

查看试题解析
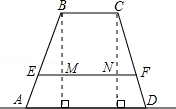23. 如图，某中学课外活动小组的同学利用所学知识去测量某河段的宽度.小明同学在A处观测对岸C点，测得 $∠ C A D = 45 °$ ，小英同学在距A处50米远的B处测得 $∠ C B D = 30 °$ ，请你根据这些数据计算出河宽.

查看试题解析
24. 如图，一位运动员在距篮下4米处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.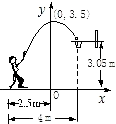

(1)、建立如图所示的直角坐标系，求抛物线的表达式；

(2)、该运动员身高1.8米，在这次跳投中，球在头顶上方0.25米处出手，问：球出手时，他跳离地面的高度是多少？

查看试题解析
25. 已知：如图，点D在三角形ABC的AB上，DE交AC于点E， $∠ A D E = ∠ B$ ，点F在AD上，且 $A D^{2} = A F \cdot A B$ .求证：

(1)、 $\frac{A D}{A B} = \frac{A E}{A C}$ ；

(2)、 $△ A E F$ ∽ $△ A C D$ .

查看试题解析
26. 如图，在平面直角坐标系中，直线 $y = \frac{1}{2} x + 2$ 与x轴交于点A，与y轴交于点C.抛物线 $y = a x^{2} + b x + c$ 的对称轴是 $x = - \frac{3}{2}$ ，且经过A、C两点，与x轴的另一交点为点B.

(1)、求出点A、B的坐标；

(2)、求抛物线解析式.

(3)、若点P为直线AC上方的抛物线上的一点，作 $P Q ⊥ x$ 轴，交AC于点Q.求线段PQ的最大值，并求出此时点P的坐标.

查看试题解析