广西桂林市灌阳县2021-2022学年九年级上学期期末考试数学试卷
试卷更新日期:2022-03-02 类型:期末考试
一、单选题
-
1. 下列方程中,关于x的一元二次方程的是( )A、x2-1=2x B、x3+2x2=0 C、 D、x2-y+1=02. 已知点 在反比例函数 的图象上,则a的值为( )A、-2 B、2 C、-3 D、33. 将一个三角形的各边都缩小到原来的 后,得到三角形与原三角形( )A、一定不相似 B、不一定相似 C、无法判断是否相似 D、一定相似4. 质检部门从同一批次1000件产品中随机抽取100件进行检测,检测出次品3件,由此估计这一批次产品中次品件数是( )A、60 B、30 C、600 D、3005. 如图,已知直线 ,直线m、n与a、b、c分别交于点A、C、E、B、D、F,若 , , ,则 的值是( )
 A、15 B、10 C、14 D、96. 下列对一元二次方程x2-2x-4=0根的情况的判断,正确的是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断7. 如图,在平面直角坐标系中,点A坐标为 ,那么 的值是( )
A、15 B、10 C、14 D、96. 下列对一元二次方程x2-2x-4=0根的情况的判断,正确的是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断7. 如图,在平面直角坐标系中,点A坐标为 ,那么 的值是( ) A、 B、 C、 D、8. 函数 与 在同一坐标系的图象大致是图中的( )A、
A、 B、 C、 D、8. 函数 与 在同一坐标系的图象大致是图中的( )A、 B、
B、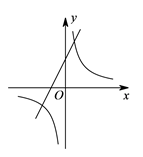 C、
C、 D、
D、 9. 某人沿着倾斜角为 ,坡度为 的斜坡向上前进了 ,那么他的高度上升了( )A、 B、 C、 D、10. 2020年10月,新田县中小学生田径运动会,甲、乙、丙、丁四位运动员在“100米短跑”训练中,每人各跑5次,据统计,平均成绩都是13.8秒,方差分别是 =0.11, =0.03, , ,则四人的训练成绩最稳定的是( )A、 甲 B、乙 C、丙 D、丁11. 如图,学校生物试验园地是长20米,宽15米的长方形,为便于管理,现要在中间开辟一横两纵三条宽均为x米的小道,要使种植面积为252平方米.则列方程为( )
9. 某人沿着倾斜角为 ,坡度为 的斜坡向上前进了 ,那么他的高度上升了( )A、 B、 C、 D、10. 2020年10月,新田县中小学生田径运动会,甲、乙、丙、丁四位运动员在“100米短跑”训练中,每人各跑5次,据统计,平均成绩都是13.8秒,方差分别是 =0.11, =0.03, , ,则四人的训练成绩最稳定的是( )A、 甲 B、乙 C、丙 D、丁11. 如图,学校生物试验园地是长20米,宽15米的长方形,为便于管理,现要在中间开辟一横两纵三条宽均为x米的小道,要使种植面积为252平方米.则列方程为( ) A、(20-x)(15-x)=252 B、(20-2x)(15-x)=252 C、(20+x)(15+x)=252 D、(20-2x)(15-x)+2x2=25212. 如图,已知点E是矩形ABCD对角线AC上的一动点,正方形EFGH的顶点G、H都在边BC上,若AB=3,BC=4,则tan∠CFE 的值( )
A、(20-x)(15-x)=252 B、(20-2x)(15-x)=252 C、(20+x)(15+x)=252 D、(20-2x)(15-x)+2x2=25212. 如图,已知点E是矩形ABCD对角线AC上的一动点,正方形EFGH的顶点G、H都在边BC上,若AB=3,BC=4,则tan∠CFE 的值( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若反比例函数 的反比例系数是.14. 在一元二次方程 中,一次项的系数是.15. 在统计学中,样本的方差可以近似地反映总体的.(在①“集中趋势”,②“波动大小”,③“平均值”,④“最大值”中选择合适的序号填写在横线上)16. 如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为点D,E,则图中与△ABC相似的三角形个数有个.
 17. 如图,在平面直角坐标系中,反比例函数 的图象上有A、B两点,它们的横坐标分别为2和4, 的面积为6,则k的值为.
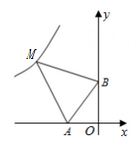
17. 如图,在平面直角坐标系中,反比例函数 的图象上有A、B两点,它们的横坐标分别为2和4, 的面积为6,则k的值为. 18. 如图,在坐标系中,以坐标原点 O, A (-8,0), B (0,6)为顶点的Rt△AOB ,其两个锐角对应的外角平分线相交于点M,且点M恰好在反比例函数 的图象上,则k的值为.
18. 如图,在坐标系中,以坐标原点 O, A (-8,0), B (0,6)为顶点的Rt△AOB ,其两个锐角对应的外角平分线相交于点M,且点M恰好在反比例函数 的图象上,则k的值为.
三、解答题
-
19. 计算:20. 解方程: .21. 在正方形网格中,每个小正方形的边长为1,△ABC在平面直角坐标系中的位置如图所示.
 (1)、画出△ABC沿x轴翻折后的△AB1C;(2)、以点M为位似中心,在网格中作出△AB1C的位似图形△A2B2C2 , 使其位似比为2:1;(3)、点A2的坐标;△ABC与△A2B2C2的周长比是.22. 市某区在今年四月开始了第一剂新冠疫苗接种,为了解疫苗的安全、有效情况,从全区已接种市民中随机抽取部分市民进行调查.调查结果根据年龄x(岁)分为四类:A类:18≤x<30;B类:30≤x<40;C类:40≤x<50;D类:50≤x≤59.现将调查结果绘制成如下不完整的统计图,请根据统计图中的信息解答下列问题:
(1)、画出△ABC沿x轴翻折后的△AB1C;(2)、以点M为位似中心,在网格中作出△AB1C的位似图形△A2B2C2 , 使其位似比为2:1;(3)、点A2的坐标;△ABC与△A2B2C2的周长比是.22. 市某区在今年四月开始了第一剂新冠疫苗接种,为了解疫苗的安全、有效情况,从全区已接种市民中随机抽取部分市民进行调查.调查结果根据年龄x(岁)分为四类:A类:18≤x<30;B类:30≤x<40;C类:40≤x<50;D类:50≤x≤59.现将调查结果绘制成如下不完整的统计图,请根据统计图中的信息解答下列问题: (1)、本次随机抽取的市民中<40岁的有人;(2)、图2中D类区域对应圆心角的度数是度;(3)、请补全条形统计图;(4)、若本次抽取人数占已接种市民人数的 5%,估计该区已接种第一剂新冠疫苗的市民有多少人?23. 某口罩生产厂家今年9月份生产口罩的数量为200万个,11月份生产口罩的数量达到242万个,且从9月份到11月份,每月的平均增长率都相同.(1)、求每月生产口罩的平均增长率;(2)、按照这个平均增长率,预计12月份这口罩生产厂家生产口罩的数量达到多少万个?24. 如图,如图,一楼房AB后有一假山CD的坡度为i=1:2,山坡坡面上E点处有一休息亭,测得假山脚与楼房水平距离BC=24米,与亭子距离CE=8 米,小丽从楼房房顶测得E的俯角为45°.
(1)、本次随机抽取的市民中<40岁的有人;(2)、图2中D类区域对应圆心角的度数是度;(3)、请补全条形统计图;(4)、若本次抽取人数占已接种市民人数的 5%,估计该区已接种第一剂新冠疫苗的市民有多少人?23. 某口罩生产厂家今年9月份生产口罩的数量为200万个,11月份生产口罩的数量达到242万个,且从9月份到11月份,每月的平均增长率都相同.(1)、求每月生产口罩的平均增长率;(2)、按照这个平均增长率,预计12月份这口罩生产厂家生产口罩的数量达到多少万个?24. 如图,如图,一楼房AB后有一假山CD的坡度为i=1:2,山坡坡面上E点处有一休息亭,测得假山脚与楼房水平距离BC=24米,与亭子距离CE=8 米,小丽从楼房房顶测得E的俯角为45°.
(1)、求点E到水平地面的距离;(2)、求楼房AB的高.25. 如图,已知一次函数 与反比例函数 的图象在第一、三象限分别交于A(6,1),B(a,-3)两点,连接OA,OB.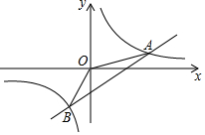 (1)、求一次函数和反比例函数的解析式;(2)、求△AOB的面积;(3)、直接写出当 时自变量x的取值范围.26. 如图1,在△ABC中,AB = AC =10,tanB = ,点D为BC 边上的动点(点D不与点B ,C重合).以D为顶点作∠ADE =∠B ,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)、求一次函数和反比例函数的解析式;(2)、求△AOB的面积;(3)、直接写出当 时自变量x的取值范围.26. 如图1,在△ABC中,AB = AC =10,tanB = ,点D为BC 边上的动点(点D不与点B ,C重合).以D为顶点作∠ADE =∠B ,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF. (1)、当D运动到BC的中点时,直接写出AF的长;(2)、求证:10CE=BD∙CD;(3)、点D在运动过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
(1)、当D运动到BC的中点时,直接写出AF的长;(2)、求证:10CE=BD∙CD;(3)、点D在运动过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.