江苏省镇江市2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-03-02 类型:期末考试
一、填空题
-
1. 的相反数是.2. 单项式 的次数是.3. 图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为5,则 .
 4. 若单项式 与 是同类项,则 的值是.5. 一个整数6250…0用科学记数法表示为 ,则原数中“0”的个数为.6. 若2a−b=1,则4a−2b+2的值为.7. 若 ,则 的余角为度.8. 如图,已知点O在直线AB上, ,则 .
4. 若单项式 与 是同类项,则 的值是.5. 一个整数6250…0用科学记数法表示为 ,则原数中“0”的个数为.6. 若2a−b=1,则4a−2b+2的值为.7. 若 ,则 的余角为度.8. 如图,已知点O在直线AB上, ,则 . 9. 数轴上点A表示的数是 ,将点A在数轴上平移5个单位长度得到点B.则点B表示的数是.10. 有理数 、 、 在数轴上位置如图,则 的值为 .
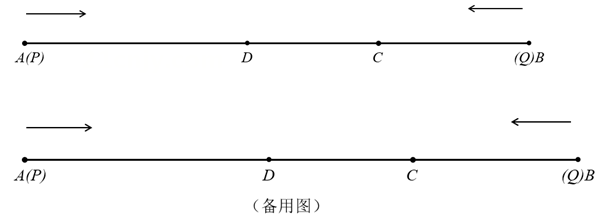
9. 数轴上点A表示的数是 ,将点A在数轴上平移5个单位长度得到点B.则点B表示的数是.10. 有理数 、 、 在数轴上位置如图,则 的值为 . 11. 如图,在一条可以折叠的数轴上,A、B两点表示的数分别是 ,3,以点C为折点,将此数轴向右对折,若点A折叠后在点B的右边,且 ,则C点表示的数是.
11. 如图,在一条可以折叠的数轴上,A、B两点表示的数分别是 ,3,以点C为折点,将此数轴向右对折,若点A折叠后在点B的右边,且 ,则C点表示的数是.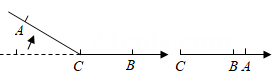 12. 如图,四边形ABCD与EFGD都是长方形,点E、G分别在AD与CD上.若 cm,长方形EFGD的周长为24cm,则图中阴影部分的面积为 .
12. 如图,四边形ABCD与EFGD都是长方形,点E、G分别在AD与CD上.若 cm,长方形EFGD的周长为24cm,则图中阴影部分的面积为 .
二、单选题
-
13. 下列计算正确的是( )A、 B、 C、 D、14. 下列图形中,可以折叠成棱锥的是( )A、
 B、
B、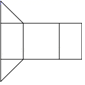 C、
C、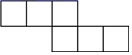 D、
D、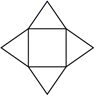 15. 下列各数: , ,0, ,3.14,其中无理数有( )A、1个 B、2个 C、3个 D、4个16. 如图,将一块三角形纸片剪去一部分后,发现剩余阴影部分的纸片周长要比原三角形纸片的周长大,能正确解释这一现象的数学知识是( )
15. 下列各数: , ,0, ,3.14,其中无理数有( )A、1个 B、2个 C、3个 D、4个16. 如图,将一块三角形纸片剪去一部分后,发现剩余阴影部分的纸片周长要比原三角形纸片的周长大,能正确解释这一现象的数学知识是( ) A、直线没有端点,向两端无限延伸 B、两点之间,线段最短 C、经过一点有无数条直线 D、两点确定一条直线17. 对于代数式 的值,下列说法正确的是( )A、比 大 B、比 小 C、比m大 D、比m小18. 要使多项式 化简后不含x的二次项,则m等于( )A、0 B、 C、 D、219. 代数式 当中,当x取值分别为 ,0,1,2时,对应代数式的值如下表:
A、直线没有端点,向两端无限延伸 B、两点之间,线段最短 C、经过一点有无数条直线 D、两点确定一条直线17. 对于代数式 的值,下列说法正确的是( )A、比 大 B、比 小 C、比m大 D、比m小18. 要使多项式 化简后不含x的二次项,则m等于( )A、0 B、 C、 D、219. 代数式 当中,当x取值分别为 ,0,1,2时,对应代数式的值如下表:x
…
0
1
2
…
…
1
3
5
…
则 的值为( )
A、 B、2 C、 D、20. 如图, 在 的内部,且 ,若 的度数是一个正整数,则图中所有角的度数之和可能是( ) A、340° B、350° C、360° D、370°
A、340° B、350° C、360° D、370°三、解答题
-
21. 计算(1)、(2)、(3)、先化简,再求值: 其中 , .22. 解方程:(1)、(2)、23. 如图,是由几个大小完全相同的小正方体垒成的几何体.
 (1)、请分别画出你所看到的三视图;(2)、若现在你手头还有一些相同的小正方体,如果保持俯视图和主视图不变,最多可以再添加个小正方体.24. 某机械加工厂计划在规定期限内完成一批零件的生产任务,如果每天生产零件25个,那么到期将比原计划少生产100个;如果每天生产零件30个,那么到期将比原计划多生产80个,求原计划几天完成任务?25. 如图,方格纸中每个小正方形的边长都是1.(1)、过点P画 ,PM与直线AB相交于点M;
(1)、请分别画出你所看到的三视图;(2)、若现在你手头还有一些相同的小正方体,如果保持俯视图和主视图不变,最多可以再添加个小正方体.24. 某机械加工厂计划在规定期限内完成一批零件的生产任务,如果每天生产零件25个,那么到期将比原计划少生产100个;如果每天生产零件30个,那么到期将比原计划多生产80个,求原计划几天完成任务?25. 如图,方格纸中每个小正方形的边长都是1.(1)、过点P画 ,PM与直线AB相交于点M; (2)、若点N在图中的格点上(不与点A重合),且直线NA与直线AC垂直,这样的格点(图中)有个;(3)、连接PB、PC,则四边形PBAC的面积是.
(2)、若点N在图中的格点上(不与点A重合),且直线NA与直线AC垂直,这样的格点(图中)有个;(3)、连接PB、PC,则四边形PBAC的面积是.