湖南省长沙市长郡教育集团2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-03-02 类型:期末考试
一、单选题
-
1. 在有理数 , , ,0中,最大的数是( )A、0 B、 C、 D、2. 2021年国庆黄金周非比寻常,七天长假期间,全国共接待国内游客约650000000人次,按可比口径同比恢复80%以上.将数据650000000用科学记数法表示应为( )A、 6.5×108 B、6.5×109 C、65.0×107 D、0.65×1093. 下列运算正确的是( )A、 B、 C、 D、4. 若当 时, ,则当 时,多项式 的值为( )A、 B、 C、 D、5. 在代数式﹣2x,x+1,π, ,0, mn中是单项式的有( )个.A、1 B、2 C、3 D、46. 下列不是正方体侧面展开图的是( )A、
 B、
B、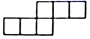 C、
C、 D、
D、 7. 若(m-1)x|m|=7是关于x的一元一次方程,则m=( )A、1 B、-1 C、±1 D、08. 下列变形中,不正确的是( )A、若a﹣3=b﹣3,则a=b B、若 ,则a=b C、若a=b,则 D、若ac=bc,则a=b9. 某商场购进一批服装,每件服装销售的标价为400元,由于换季滞销,商场决定将这种服装按标价的六折销售,若打折后每件服装仍能获利20%,则该服装的进价是( )A、160元 B、180元 C、200元 D、220元10. 如图所示,由A到B有①、②、③三条路线,最短的路线选①的理由是( )
7. 若(m-1)x|m|=7是关于x的一元一次方程,则m=( )A、1 B、-1 C、±1 D、08. 下列变形中,不正确的是( )A、若a﹣3=b﹣3,则a=b B、若 ,则a=b C、若a=b,则 D、若ac=bc,则a=b9. 某商场购进一批服装,每件服装销售的标价为400元,由于换季滞销,商场决定将这种服装按标价的六折销售,若打折后每件服装仍能获利20%,则该服装的进价是( )A、160元 B、180元 C、200元 D、220元10. 如图所示,由A到B有①、②、③三条路线,最短的路线选①的理由是( )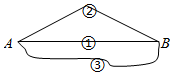 A、两点确定一条直线 B、两点间距离的定义 C、两点之间,线段最短 D、因为它直11. 如图,点 在直线 上, ,那么下列说法错误的是( )
A、两点确定一条直线 B、两点间距离的定义 C、两点之间,线段最短 D、因为它直11. 如图,点 在直线 上, ,那么下列说法错误的是( ) A、 与 相等 B、 与 互余 C、 与 互补 D、 与 互余12. 如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒).若点P在运动过程中,当PB=2时,则运动时间t的值为( )
A、 与 相等 B、 与 互余 C、 与 互补 D、 与 互余12. 如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒).若点P在运动过程中,当PB=2时,则运动时间t的值为( ) A、 秒或 秒 B、 秒或 秒或 秒或 秒 C、3秒或7秒或 秒或 秒 D、 秒或 秒或 秒或 秒
A、 秒或 秒 B、 秒或 秒或 秒或 秒 C、3秒或7秒或 秒或 秒 D、 秒或 秒或 秒或 秒二、填空题
-
13. 的相反数为.14. 若2x4yn与-5xmy是同类项,则nm=.15. 定义运“#”运法则为:x#y=y﹣2,则(4#2)#(﹣3)=.16. 一艘轮船在水中由 地开往 地,顺水航行用了4小时,由 地开往 地,逆水航行比顺水航行多用了1小时,已知此船在静水中速度是18千米/时,水流速度为千米/小时.17. 如图,已知线段AB=16 cm,M是AB的中点,P是线段MB上一点,N为PB的中点,NB=3 cm,则线段MP=cm.
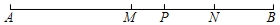 18. 如图,在∠AOB的内部有3条射线OC、OD、OE,若∠AOC=70°,∠BOE= ∠BOC,∠BOD= ∠AOB,则∠DOE=°.(用含n的代数式表示)
18. 如图,在∠AOB的内部有3条射线OC、OD、OE,若∠AOC=70°,∠BOE= ∠BOC,∠BOD= ∠AOB,则∠DOE=°.(用含n的代数式表示)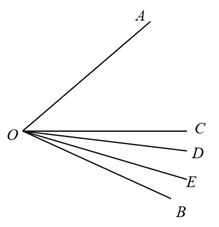
三、解答题
-
19. 解方程:(1)、9x﹣7=2(3x+4)(2)、20. 计算:21. 先化简,再求值: ,其中22. 如图是由几个相同的边长为1个单位的小立方块搭成的几何体从上面看到的形状,方格中的数字表示该位置的小立方块的个数.
 (1)、请在方格纸中分别画出从正面和左面所观察到的几何体的形状;(2)、由三个不同方向所观察到的图形可知这个组合几何体的表面积为个平方单位(包括底面积).23. 小李在解关于x的方程 -1去分母时,方程右边的-1漏乘了3,因而求得方程的解为x=-2,请你帮小李同学求出a的值,并且求出原方程的解.24. 如图,点C为线段AB上一点,点D为BC的中点,且AB=12,AC=4CD.
(1)、请在方格纸中分别画出从正面和左面所观察到的几何体的形状;(2)、由三个不同方向所观察到的图形可知这个组合几何体的表面积为个平方单位(包括底面积).23. 小李在解关于x的方程 -1去分母时,方程右边的-1漏乘了3,因而求得方程的解为x=-2,请你帮小李同学求出a的值,并且求出原方程的解.24. 如图,点C为线段AB上一点,点D为BC的中点,且AB=12,AC=4CD. (1)、求AC的长;(2)、若点E在直线AB上,且AE=3,求DE的长.25. 如图, 为直线 上一点, , 是 的平分线, ,
(1)、求AC的长;(2)、若点E在直线AB上,且AE=3,求DE的长.25. 如图, 为直线 上一点, , 是 的平分线, , (1)、求 的度数(2)、试判断 是否平分 ,并说明理由26. 某中学库存若干套桌椅,准备修理后支援贫困山区学校.现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费.(1)、该中学库存多少套桌椅?(2)、在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理.你认为哪种方案省时又省钱?为什么?27. 一般情况下 不成立,但有些数可以使得它成立,例如:a=b=0,我们称使得 成立的一对数a,b为“双语数对”,记为(a,b).(1)、填空:(-4,9)“双语数对”(填“是”或“否”);(2)、若(1,b)是“双语数对”,求b的值;(3)、已知(m,n)是“双语数对”,试说明 也是“双语数对”.28. 如图1,在数轴上A、B两点对应的数分别是6,-6,∠DCE=90°(C与O重合,D点在数轴的正半轴上).
(1)、求 的度数(2)、试判断 是否平分 ,并说明理由26. 某中学库存若干套桌椅,准备修理后支援贫困山区学校.现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费.(1)、该中学库存多少套桌椅?(2)、在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理.你认为哪种方案省时又省钱?为什么?27. 一般情况下 不成立,但有些数可以使得它成立,例如:a=b=0,我们称使得 成立的一对数a,b为“双语数对”,记为(a,b).(1)、填空:(-4,9)“双语数对”(填“是”或“否”);(2)、若(1,b)是“双语数对”,求b的值;(3)、已知(m,n)是“双语数对”,试说明 也是“双语数对”.28. 如图1,在数轴上A、B两点对应的数分别是6,-6,∠DCE=90°(C与O重合,D点在数轴的正半轴上). (1)、如图1,若CF平分∠ACE,则∠AOF=;(2)、如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.
(1)、如图1,若CF平分∠ACE,则∠AOF=;(2)、如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.①当t=1时,α= ▲ ;
②猜想∠BCE和α的数量关系,并证明;
(3)、如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴正半轴向右平移t(0<t<3)个单位,再绕顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1 , 记∠D1C1F1=β,若α,β满足|α-β|=75°,请求出t的值.