湖南省长沙市明德教育集团2021-2022学年七年级上学期期末考试数学试卷

试卷更新日期：2022-03-02 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣2022的绝对值等于（）

A、2022 B、﹣2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 下列关于有理数的大小比较，正确的是（）．

A、 $0 < - 1$ B、 $- 5 > - 4$ C、 $2 < - 2^{2}$ D、 $- 2 > - 3$

查看试题解析
3. 下列各式中，合并同类项正确的是（）

A、3a+a=3a² B、3x+4y=7xy C、a²+a²=a⁴ D、2m+3m=5m

查看试题解析
4. 截止2021年10月16日，电影《长津湖》票房突破4700000000元，目前票房已超《流浪地球》，成中国影史第四，4700000000元用科学记数法表示为（）

A、4.7×10⁸元 B、4.7×10⁹元 C、47×10⁸元 D、4.7×10¹⁰元

查看试题解析
5. 如图，是一个正方体的展开图，则该正方体与“国”相对面上的汉字是（）

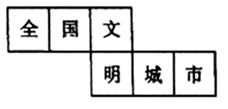A、文 B、明 C、城 D、市

查看试题解析
6. 如图，从A到B有①，②，③三条路线，最短的路线是①，其理由是（）

A、因为它最直 B、两点确定一条直线 C、两点间的距离的概念 D、两点之间，线段最短

查看试题解析
7. 下列运算中，去括号正确的是（）

A、 $- (7 a + 1) = - 7 a + 1$ B、 $- (7 a - 1) = - 7 a - 1$ C、 $- (- 7 a - 1) = 7 a + 1$ D、 $- (- 7 a - 1) = - 7 a + 1$

查看试题解析
8. 《孙子算经》中有一道题，原文是：今有三人共车，二车空：二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车：若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？设共有x人，可列方程（）

A、 $\frac{x + 2}{3} = \frac{x}{2} - 9$ B、 $\frac{x}{3} + 2 = \frac{x - 9}{2}$ C、 $\frac{x}{3} - 2 = \frac{x + 9}{2}$ D、 $\frac{x - 2}{3} = \frac{x}{2} + 9$

查看试题解析
9. 如图，甲从A处出发沿北偏东60°方向走向B处，乙从A处出发沿南偏西30°方向走到C处，则∠BAC的度数是（）

A、 $160^{\circ}$ B、 $150^{\circ}$ C、 $120^{\circ}$ D、 $90^{\circ}$

查看试题解析
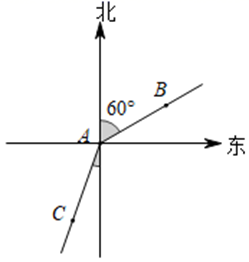10. 有理数 $a ， b ， c$ 在数轴上对应的点的位置如图所示，则下列各式正确的个数有（）
① $a b c > 0$ ；② $a + c < b$ ；③ $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = - 1$ ；④ $| a - b | - | b - c | = | a - c |$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 对于多项式 $2 x^{2} - 3 {xy}^{2} - 4$ ，它的二次项是

查看试题解析
12. 若关于 $x$ 的方程 $(n - 1) x^{| n |} + 1 = 4$ 是一元一次方程，则 $n$ 的值是

查看试题解析
13. 若 $∠ α$ =27°，则 $∠ α$ 的补角是

查看试题解析
14. 若方程 $4 x - 3 a = 2$ 和方程 $6 x - 7 = 5$ 的解相同，则 $a$ 的值是

查看试题解析
15. 已知 $a - 2 b = 2$ ，则代数式 $6 b - 3 a + 7$ 的值为

查看试题解析
16. 线段 $A B = 1$ ， $C_{1}$ 是 $A B$ 的中点， $C_{2}$ 是 $C_{1} B$ 的中点， $C_{3}$ 是 $C_{2} B$ 的中点， $C_{4}$ 是 $C_{3} B$ 的中点，依此类推……，线段 $A C_{2022}$ 的长为

查看试题解析

三、解答题

17. 计算：

(1)、 $- 24 \times (\frac{1}{3} - \frac{5}{6} - \frac{7}{12} + \frac{11}{24})$

(2)、 $- 1^{2022} + （ - 2 ）^{3} \times （ - \frac{1}{2} ） - | - 4 |$

查看试题解析
18. 已知 $| a - 2 | + {(b + 1)}^{2} = 0$ ，求 $3 (2 a^{2} b - a b^{2}) - (5 a^{2} b - 3 a b^{2})$ 的值.

查看试题解析
19. 解方程

(1)、 $5 x - 6 = 3 x + 2$

(2)、 $\frac{x - 3}{2} - 1 = \frac{4 x + 1}{5}$

查看试题解析
20. 如图，O是直线AB上一点，∠DOB=90°，∠EOC=90°.

(1)、如果∠DOE=50°，求∠BOC的度数；

(2)、若OE平分∠AOD，求∠BOE.

查看试题解析
21. 设 $A = 5 x^{2} + m x - 1$ ， $B = n x^{2} - 3 x + 3 （其中 m ， n 为系数）$ ，若 $A + 2 B$ 的值与 $x$ 的取值无关，求 $m ， n$ 的值

查看试题解析
22. 如图，点A、B、C、D在同一条直线上，且AB：BC：CD=2：3：5，线段BC=6.

(1)、求线段AB、CD的长；

(2)、若在直线上存在一点M使得AM=2，求线段DM的长.

查看试题解析
23. 春节将至，小明家亲友团准备去某地旅游，甲旅行社的优惠办法是：买4张全票其余人按半价优惠；乙旅行社的优惠办法是：一律按原价的七五折优惠；已知这两家旅行社的原价均为4000元每人.

(1)、若亲友团有6人，甲、乙旅行社各需多少费用？

(2)、亲友团为多少人时，甲、乙旅行社的费用相同？

(3)、当亲友团人数满足什么条件时，甲旅行社的收费更优惠？当亲友团人数满足什么条件时，乙旅行社的收费更优惠？（直接写出结果，不需说明理由）

查看试题解析
24. 我们规定，若关于x的一元一次方程ax=b的解为x=b-a，则称该方程为“定值方程”.例如：2x=4的解为x=2=4-2，则该方程2x=4是“定值方程”.请根据上述规定解答下列问题：

(1)、判断方程4x=6 （回答“是”或“不是”）“定值方程”；

(2)、若a=3，有符合要求的“定值方程”吗？若有，求b的值；若没有，请说明理由.

(3)、若关于x的一元一次方程2x=mn+m和-2x=mn+n都是“定值方程”，求代数式5-3m+3n的值.

查看试题解析
25. 已知∠AOD＝40°，射线OC从OD出发，绕点O以20°/秒的速度逆时针旋转，旋转时间为t秒.射线OE、OF分别平分∠AOC、∠AOD.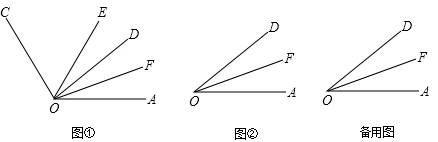

(1)、如图①：如果t＝4秒，求∠EOA的度数；

(2)、如图①：若射线OC旋转时间为t（t≤7）秒，求∠EOF的度数（用含t的代数式表示）；

(3)、若射线OC从OD出发时，射线OB也同时从OA出发，绕点O以60°/秒的速度逆时针旋转，射线OC、OB在旋转过程中（t≤3）， $∠ C O E = \frac{1}{2} ∠ B O E$ 请你借助图②与备用图进行分析后，
（i）求此时t的值；

（ii） $\frac{∠ E O F}{∠ B O C}$ 求的值.

查看试题解析