浙江省嘉兴市2021-2022学年高二上学期数学期末考试试卷

试卷更新日期：2022-03-02 类型：期末考试

进入出卷网下载

一、单选题

1. 立德中学高一年级共有学生640人，其中男生300人，现采用分层抽样的方法调查学生的身高情况，在抽取的样本中，男生有30人，那么该样本中女生的人数为（）

A、30人 B、34人 C、60人 D、64人

查看试题解析
2. 若函数 $f (x) = 3^{x} + sin 2 x$ ，则（）

A、 $f^{'} (x) = 3^{x} ln 3 + 2 cos 2 x$ B、 $f^{'} (x) = 3^{x} + 2 cos 2 x$ C、 $f^{'} (x) = 3^{x} ln 3 + cos 2 x$ D、 $f^{'} (x) = 3^{x} ln 3 - 2 cos 2 x$

查看试题解析
3. 过点 $(- 1 ， 3)$ 且垂直于直线 $x - 2 y + 3 = 0$ 的直线方程为（）

A、 $x - 2 y - 7 = 0$ B、 $2 x + y - 5 = 0$ C、 $x + 2 y - 5 = 0$ D、 $2 x + y - 1 = 0$

查看试题解析
4. 已知双曲线 $C ： \frac{x^{2}}{2} - \frac{y^{2}}{2} = 1$ 的右顶点为 $A$ ，过点 $A$ 作圆 $x^{2} + y^{2} = 1$ 的两条切线 $A M ， A N$ ，切点分别为 $M ， N$ ，则 $△ A M N$ 的面积为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{7 \sqrt{7}}{16}$ D、 $\frac{7 \sqrt{7}}{8}$

查看试题解析
5. 古希腊数学家欧几里得在《几何原本》中描述了圆锥曲线的共性，并给出了圆锥曲线的统一定义，他指出，平面内到定点的距离与到定直线的距离的比是常数 $e$ 的点的轨迹叫做圆锥曲线；当 $0 < e < 1$ 时，轨迹为椭圆；当 $e = 1$ 时，轨迹为抛物线；当 $e > 1$ 时，轨迹为双曲线.则方程 $\frac{\sqrt{{(x - 4)}^{2} + y^{2}}}{| 25 - 4 x |} = \frac{1}{5}$ 表示的圆锥曲线的离心率 $e$ 等于（）

A、 $\frac{1}{5}$ B、 $\frac{4}{5}$ C、 $\frac{5}{4}$ D、5

查看试题解析
6. 跑步是一项常见的有氧运动，能增强人体新陈代谢和基础代谢率，是治疗和预防“三高”的有效手段.赵老师最近给自己制定了一个180千米的跑步健身计划，计划前面5天中每天跑4千米，以后每天比前一天多跑0.4千米，则他要完成该计划至少需要（）

A、23天 B、24天 C、25天 D、26天

查看试题解析
7. 设 $a = e^{\sqrt{2}} - ln 2 ， b = e^{\sqrt{3}} - ln 3 ， c = \sqrt{2} e - \frac{2}{e}$ （其中 $e \approx 2.71828$ 是自然对数的底数），则（）

A、 $a < b < c$ B、 $b < a < c$ C、 $b < c < a$ D、 $c < a < b$

查看试题解析
8. 1202年，意大利数学家斐波那契出版了他的《算盘全书》.他在书中提出了一个关于兔子繁殖的问题，发现数列： $1 ， 1 ， 2 ， 3 ， 5 ， 8 ， 13 ， \dots$ ，该数列的特点是：前两项均为1，从第三项起，每一项等于前两项的和，人们把这个数列 ${F_{n}}$ 称为斐波那契数列，则下列结论正确的是（）

A、 $F_{2} + F_{4} + F_{6} + \dots + F_{2020} = F_{2021}$ B、 $F_{1}^{2} + F_{2}^{2} + F_{3}^{2} + \dots + F_{2021}^{2} = F_{2021} F_{2022}$ C、 $F_{1} + F_{2} + F_{3} + \dots + F_{2021} = F_{2023}$ D、 $F_{1} + F_{3} + F_{5} + \dots + F_{2021} = F_{2022} - 1$

查看试题解析

二、多选题

9. 已知直线 $l ： (1 + a) x + y + 1 = 0 (a \in R)$ 与圆 $C ： x^{2} + y^{2} = 1$ ，则下列结论正确的是（）

A、直线 $l$ 必过定点 B、 $l$ 与C可能相离 C、 $l$ 与C可能相切 D、当 $a = 1$ 时， $l$ 被C截得的弦长为 $\frac{4 \sqrt{5}}{5}$

查看试题解析
10. 为唤起学生爱护地球､保护家园的意识，加强对节能减排的宣传，进一步营造绿色和谐的校园环境，树人中学决定举办环保知识竞赛.现有甲､乙､丙､丁四个班级参加，每个班级各派10位同学参赛，每位同学需要回答10道题，每题回答正确得1分，回答错误得0分.若规定总得分达到70分且没有同学得分低于5分的班级为“优胜班级”，则根据以下甲､乙､丙､丁各班参赛同学的得分数据信息，能判断该班一定为“优胜班级”的是（）

A、甲班同学平均数为8，众数为8 B、乙班同学平均数为8，方差为4 C、丙班同学平均数为7，极差为3 D、丁班同学平均数为7，标准差为0

查看试题解析
11. 函数 $f (x)$ 的定义域为 $(a ， b)$ ，导函数 $f^{'} (x)$ 在 $(a ， b)$ 内的图象如图所示，则（）

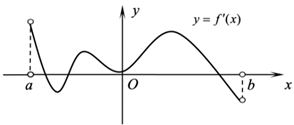A、函数 $f (x)$ 在 $(a ， b)$ 内一定不存在最小值 B、函数 $f (x)$ 在 $(a ， b)$ 内只有一个极小值点 C、函数 $f (x)$ 在 $(a ， b)$ 内有两个极大值点 D、函数 $f (x)$ 在 $(a ， b)$ 内可能没有零点

查看试题解析
12. 已知平面内两个定点 $A (- 5 ， 0) ， B (5 ， 0)$ ，直线 $A M ， B M$ 相交于点 $M$ ，且它们的斜率之积为常数 $λ (λ \neq 0)$ ，设点 $M$ 的轨迹为 $C$ .下列说法中正确的有（）

A、存在常数 $λ (λ \neq 0)$ ，使 $C$ 上所有的点到两点 $(- 6 ， 0) ， (6 ， 0)$ 的距离之和为定值 B、存在常数 $λ (λ \neq 0)$ ，使 $C$ 上所有的点到两点 $(- 6 ， 0) ， (6 ， 0)$ 的距离之差的绝对值为定值 C、存在常数 $λ (λ \neq 0)$ ，使 $C$ 上所有的点到两点 $(0 ， - 6) ， (0 ， 6)$ 的距离之和为定值 D、存在常数 $λ (λ \neq 0)$ ，使 $C$ 上所有的点到两点 $(0 ， - 6) ， (0 ， 6)$ 的距离之差的绝对值为定值

查看试题解析

三、填空题

13. 以点 $(1 ， 1)$ 为圆心且与直线 $x - 3 = 0$ 相切的圆的方程是.

查看试题解析
14. 已知数列 ${a_{n}}$ 的通项公式 $a_{n} = 2^{n} - 1$ ，则其前 $n$ 项和 $S_{n} =$ .

查看试题解析
15. 已知椭圆 $C ： \frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ ，双曲线D与椭圆 $C$ 共焦点，且与椭圆C在四个象限的交点分别为 $M ， N ， P ， Q$ ，则四边形 $M N P Q$ 面积的最大值是.

查看试题解析
16. 已知不等式 $(a x - ln x) (e^{x} - a x) \geq 0$ 对任意 $x > 0$ 恒成立（其中 $e \approx 2.71828$ 是自然对数的底数），则实数 $a$ 的取值范围是.

查看试题解析

四、解答题

17. 已知数列 ${a_{n}}$ 为公差不为零的等差数列， $a_{1} = 1$ ，记 $S_{n}$ 为其前 $n$ 项和，___________.给出下列三个条件：条件① $S_{100} = 10000$ ；条件② $a_{2} ， a_{5} ， a_{14}$ 成等比数列；条件③ ${(- 1)}^{1} a_{1} + {(- 1)}^{2} a_{2} + {(- 1)}^{3} a_{3} + \dots + {(- 1)}^{2022} a_{2022} = 2022$ .试在这三个条件中任选一个，补充在上面的横线上，完成下列两问的解答：

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \frac{1}{a_{n} a_{n + 1}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ .
注：如果选择多个条件解答，按第一个解答计分.

查看试题解析
18. 从某城市抽取100户居民进行月用电量调查，发现他们的用电量都在50到350度之间，将数据按照 $[50 ， 100) ， [100 ， 150) ， \dots ， [300 ， 350]$ 分成6组，画出的频率分布直方图如下图所示.

(1)、求直方图中的 $x$ 值和月平均用电量的众数；

(2)、已知该市有200万户居民，估计居民中用电量落在区间 $[100 ， 250)$ 内的总户数，并说明理由.

查看试题解析
19. 已知圆 $C_{1} ： x^{2} + y^{2} + 2 x + 8 y - 8 = 0$ ，圆 $C_{2} ： {(x - a)}^{2} + {(y - 2 a + 2)}^{2} = 25$ .

(1)、若圆 $C_{1}$ 与圆 $C_{2}$ 外切，求实数 $a$ 的值；

(2)、若圆 $C_{1}$ 与圆 $C_{2}$ 相交于 $A ， B$ 两点，弦AB的长为 $\sqrt{55}$ ，求实数 $a$ 的值.

查看试题解析
20. 已知首项为 $\frac{1}{2}$ 的等比数列 ${a_{n}}$ 是递减数列，其前 $n$ 项和为 $S_{n}$ ，且 $S_{1} + a_{1} ， S_{3} + a_{3} ， S_{2} + a_{2}$ 成等差数列，数列 ${b_{n}}$ 满足 $b_{1} = 1 ， n b_{n + 1} - (n + 1) b_{n} = n (n + 1)$ .

(1)、求数列 ${a_{n}} ， {b_{n}}$ 的通项公式；

(2)、设数列 ${a_{n} \sqrt{b_{n}}}$ 的前 $n$ 项和为 $T_{n}$ ，证明： $T_{n} < 2$ .

查看试题解析
21. 如图，已知点 $P$ 是拋物线 $C ： y^{2} = 2 p x (p > 0)$ 的准线 $l ： x = - 1$ 上的动点，拋物线C上存在不同的两点 $A ， B$ 满足 $P A ， P B$ 的中点均在C上.

(1)、求拋物线C的方程；

(2)、记直线 $P A ， P B ， P O$ 的斜率分别为 $k_{1} ， k_{2} ， k_{3}$ ，请问是否存在常数 $λ$ ，使得 $\frac{1}{k_{1}} + \frac{1}{k_{2}} = λ k_{3}$ ？若存在，求出 $λ$ 的值；若不存在，请说明理由.

查看试题解析
22. 已知函数 $f (x) = x ln (x + 2)$ .

(1)、求函数 $f (x)$ 在点 $(0 ， f (0))$ 处的切线方程；

(2)、若 $x_{1} ， x_{2}$ 为方程 $f (x) = k$ 的两个不相等的实根，证明：
（i） $f (x) ⩾ - x - 1$ ；

（ii） $| x_{1} - x_{2} | \leq (1 + \frac{1}{ln 2}) k + 1$ .

查看试题解析