浙江省杭州市八县区2021-2022学年高二上学期数学期末学业水平测试试卷

试卷更新日期：2022-03-02 类型：期末考试

进入出卷网下载

一、单选题

1. 全集 $U = {0 ， - 1 ， - 2 ， - 3 ， - 4}$ ， $M = {0 ， - 1 ， - 2} ， N = {0 ， - 3 ， - 4}$ ，则 $(C_{U} M) \cap N =$ （）

A、{0} B、 ${- 3 ， - 4}$ C、 ${- 1 ， - 2}$ D、 $\emptyset$

查看试题解析
2. 若复数z满足 $z (1 + 2 i) = 3 - 4 i$ （其中i为虚数单位），则z的虚部是（）

A、2i B、 $- 2 i$ C、2 D、-2

查看试题解析
3. 已知 $x^{2} + y^{2} - 6 x - 7 = 0$ 与抛物线 $y = a x^{2} (a > 0)$ 的准线相切．则 $a =$ （）

A、 $\frac{1}{16}$ B、16 C、 $\frac{1}{8}$ D、8

查看试题解析
4. 下列命题中，不正确的是（）

A、若事件A，B互斥，则 $P (A \cup B) = P (A) + P (B)$ B、若事件A，B互为独立，则 $P (\bar{A} \bar{B}) = P (\bar{A}) P (\bar{B})$ C、若事件A，B，C两两互斥，则 $P (A \cup B \cup C) = P (A) + P (B) + P (C)$ D、若事件A，B，C两两独立，则 $P (A B C) = P (A) P (B) P (C)$

查看试题解析
5. 如图所示，是某厂生产的一批不倒翁型台灯外形，它由一个圆锥和一个半球组合而成，其中，圆锥的底面和球的直径都是0.2m，圆锥的高是0.24m．要对1000个这样的台灯表面涂一层胶，如果每平方米需要涂胶100克，则共需胶（）克

A、340π B、440π C、4600π D、6600π

查看试题解析
6. 已知函数 $f (x) = \sin (ω x + φ)$ （ $ω > 0$ ， $| φ | < π$ ），其图象关于点 $(- \frac{π}{6} ， 0)$ 成中心对称，相邻两条对称轴的距离为 $\frac{π}{2}$ ，且对任意 $x \in R$ ，都有 $f (x) \geq f (\frac{7}{12} π)$ ，则在下列区间中，f(x)为单调递减函数的是（）

A、 $[- \frac{π}{6} ， \frac{π}{3}]$ B、 $[0 ， \frac{7 π}{12}]$ C、 $[\frac{π}{12} ， \frac{π}{2}]$ D、 $[\frac{7 π}{12} ， π]$

查看试题解析
7. 已知函数 $f (x) = 2^{x} + x$ ， $g (x) = \log_{2} x + x$ ， $h (x) = x^{2} + \log_{2} x$ 的零点分别为a，b，c，下列各式正确的是（）

A、 $a + b > 0$ B、 $2^{a} + \log_{2} b > 0$ C、 $b > c$ D、 $2^{a} > c^{2}$

查看试题解析
8. a为实数，函数 $f (x) = | x^{2} - 2 a x |$ 在区间[0，1]上的最大值记为g（a）．当g（a）取得最小值时， $a =$ （）

A、 $\sqrt{2} - 1$ B、 $\sqrt{2} + 1$ C、 $\pm \sqrt{2} - 1$ D、1

查看试题解析

二、多选题

9. 若椭圆的焦点为 $F_{1} (- c ， 0)$ ， $F_{2} (c ， 0)$ $(c > 0)$ ，长轴长为2a，则椭圆上的点（x，y）满足（）

A、 $\sqrt{{(x + c)}^{2} + y^{2}} + \sqrt{{(x - c)}^{2} + y^{2}} = 2 a$ B、 $\frac{y^{2}}{x^{2} - a^{2}} = \frac{c^{2}}{a^{2}} - 1$ C、 $\frac{\sqrt{{(x - c)}^{2} + y^{2}} - 1}{| \frac{a^{2}}{c} - x |} = \frac{c}{a}$ D、 $\sqrt{{(x - c)}^{2} + y^{2}} = a - \frac{c}{a} x$

查看试题解析
10. 设α，β为两个平面，则 $α ∥ β$ 的必要不充分条件是（）

A、α内有无数条直线与β平行 B、α内有两条相交直线与β平行． C、α，β垂直于同一条直线 D、α，β垂直于同一平面

查看试题解析
11. 已知点A、B、P在 $⊙ C$ 上，则下列命题中正确的是（）

A、 $| \vec{A C} | = 1$ ，则 $\vec{A C} \cdot \vec{A B}$ 的值是 $\frac{1}{2}$ B、 $| \vec{A B} | = 1$ ，则 $\vec{A C} \cdot \vec{A B}$ 的值是 $\frac{1}{2}$ C、 $| \vec{A C} | = | \vec{A B} | = 1$ ，则 $\vec{A P} \cdot \vec{A B}$ 的范围是 $[- \frac{1}{2} ， \frac{3}{2}]$ D、 $| \vec{A C} | = | \vec{A B} | = 1$ ，且 $\vec{A P} = λ \vec{A B} + μ \vec{A C}$ ，则 $λ + μ$ 的范围是 $[1 - \frac{2 \sqrt{3}}{3} ， 1 + \frac{2 \sqrt{3}}{3}]$

查看试题解析
12. 定义全集U的子集M的特征函数 $f_{M} (x) = {\begin{array}{l} 1 ， x \in M \\ 0 ， x \in ∁_{U} M \end{array}$ ．已知 $A \subseteq U$ ， $B \subseteq U$ ，则以下结论中正确的是（）

A、若 $A \subseteq B$ ，则对于任意 $x \in U$ ，都有 $f_{A} (x) \leq f_{B} (x)$ B、对于任意 $x \in U$ ，都有 $f_{∁_{U} A} (x) = 1 - f_{A} (x)$ C、对于任意 $x \in U$ ，都有 $f_{A \cap B} (x) = f_{A} (x) \cdot f_{B} (x)$ D、对于任意 $x \in U$ ，都有 $f_{A \cup B} (x) = f_{A} (x) + f_{B} (x)$

查看试题解析

三、填空题

13. $\log_{3} \frac{1}{9} + 4^{- \frac{1}{2}} =$ ．

查看试题解析
14. 已知 $\tan α = - \frac{1}{3}$ ， $2 π < α < 3 π$ ，则 $\sin α =$ ．

查看试题解析
15. 某地现有耕地10000公顷．规划10年后粮食单产比现在增加20%，人均粮食占有量比现在至少提高16%．如果人口年增长率为3%（即千分之三），那么耕地平均每年至多只能减少公顷（精确到小数点后一位， ${1.003}^{10} \approx 1.0304$ ）．
（备注：粮食单产 $= \frac{总产量}{耕地面积}$ ，人均粮食占有量 $= \frac{总产量}{总人口数}$ ）

查看试题解析
16. 过抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点F的直线交抛物线于A，B两点，点C在直线 $x = - \frac{p}{2}$ 上，则 $∠ A C B$ 的最大值是；若 $△ A C B$ 为正三角形，则其边长为．

查看试题解析

四、解答题

17. 已知a，b，c分别为 $△ A B C$ 的三个内角A，B，C的对边，在① $a \sin B = \sqrt{3} b \cos A$ ，② $2 a \cos A = b \cos C + c \cos B$ ，③ $(a + b) (\sin A - \sin B) = (c - b) \sin C$ 这三个条件中任选一个，并解答下列问题（如果选择多个条件分别解答，按第一个解答计分）：

(1)、求角A；

(2)、若 $b = 5$ ， $c = 3$ ，求BC边上的中线长．

查看试题解析
18. 某城市为节能减排，提出了在保障生活必需的基础上，“低碳生活，节约用电”的倡议．以下是某社区随机提取的100户居民的月平均用电量（单位：度）的数据，根据这些数据，以[160，180），[180，200），[200，240），[240，260），[260，280），[280，300]分组的频率分布直方图如图所示．

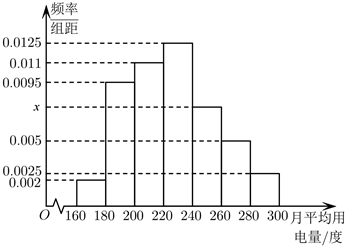(1)、求月平均用电量的25%分位数（精确到小数点后1位）；

(2)、在月平均用电量最小组[160，180）和最大组[280，300]用户中，各随机抽取1户到社区做用电情况交流，其中最小组的甲与最大组的乙恰有一人被选到的概率．

查看试题解析
19. 莱昂哈德·欧拉（Leonhard Euler，瑞士数学家），1765年在他的著作《三角形的几何学》中首次提出定理：三角形的重心（三条中线的交点）、垂心（三条高线的交点）和外心（三条中垂线的交点）共线．这条线被后人称为三角形的欧拉线．已知 $△ Q M N$ 的顶点 $M (1 ， 0)$ ， $N (3 ， - 2)$ ， $Q (1 ， - 4)$ ．

(1)、求 $△ Q M N$ 的欧拉线方程；

(2)、记 $△ Q M N$ 的外接圆的圆心为C，直线l： $k x - y - k - 1 = 0 (k \in R)$ 与圆C交于A，B两点，且 $C \notin l$ ，求 $△ A B C$ 的面积最大值．

查看试题解析
20. 如图，在四棱锥P—ABCD中，底面ABCD是正方形，侧棱 $P D ⊥$ 底面ABCD，二面角P—BC—A的大小是45°，E、G分别是PC、PA的中点， $E F ⊥ P B$ 交PB于点F．

(1)、求证：D、E、F、G四点共面；

(2)、设Q是直线AD的中点，求直线FQ与平面DFG所成角的正弦值．

查看试题解析
21. 已知双曲线C的离心率 $e = \sqrt{3}$ ，左焦点 $F_{1} (- c ， 0)$ 到其渐近线的距离为 $\sqrt{6}$ ．

(1)、求双曲线C的方程；

(2)、设T是y轴上的点，过T作两直线分别交双曲线C的左支于P、Q两点和A、B两点，若 $\frac{| T A |}{| T B |} = \frac{| T P |}{| T Q |}$ ，P、Q两点的中点为M，A、B两点的中点为N，O为坐标原点，求两直线OM和ON的斜率之和．

查看试题解析
22. 我们知道，函数 $y = f (x)$ 的图象关于坐标原点成中心对称图形的充要条件是函数 $y = f (x)$ 为奇函数，有同学发现了更一般结论：函数 $y = f (x)$ 的图象关于点 $P (a ， b)$ 成中心对称图形的充要条件是函数 $y = f (x + a) - b$ 为奇函数，试根据此结论解答下列问题：

(1)、若函数 $y = g (x)$ 满足对任意的实数m，n，恒有 $g (m + n) = g (m) + g (n) - 1$ ，求 $g (0)$ 的值，并判断此函数图象是否中心对称图形？若是，请求出对称中心坐标；

(2)、若（1）中的函数还满足 $m > 0$ 时， $g (m) > 1$ ，求不等式 $g (3 x^{2} - 2 x - 1) > 1$ 的解集；

(3)、若函数 $h (x) = \frac{2 \cdot 3^{x}}{3^{x} + 1}$ ．若 $h (x)$ 与 $g (x)$ 的图象有3个不同的交点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ， $C (x_{3} ， y_{3})$ 其中 $x_{1} < x_{2} < x_{3}$ ，且 $| A C | = \frac{4 \sqrt{29}}{5}$ ，求 $g (1)$ 值．

查看试题解析