人教版数学九年级图形的认识专题训练
试卷更新日期:2022-03-02 类型:二轮复习
一、单选题
-
1. 下列长度的三条线段能组成三角形的是( )A、3cm,5cm,6cm B、3cm,3cm,6cm C、3cm,4 cm,8cm D、4cm,5cm,1cm2. 如图.AB=AC,BD=1,BD⊥AD,则数轴上点C所表示的数为( )
 A、 +1 B、- -1 C、- +1 D、 -13. 如图,在△ABC中,AB=AC,BE=CD,BD=CF,若∠A=40°,则∠EDF等于( )
A、 +1 B、- -1 C、- +1 D、 -13. 如图,在△ABC中,AB=AC,BE=CD,BD=CF,若∠A=40°,则∠EDF等于( ) A、40° B、50° C、60° D、70°4. 如图, 是 的直径, 是弦, , 则 的度数是( )
A、40° B、50° C、60° D、70°4. 如图, 是 的直径, 是弦, , 则 的度数是( )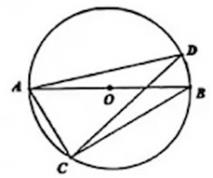 A、 B、 C、 D、5. 如图,P为正六边形 边上一动点,点P从点D出发,沿六边形的边以1cm/s的速度按逆时针方向运动,运动到点C停止.设点P的运动时间为 ,以点P、C、D为顶点的三角形的面积是 ,则下列图象能大致反映y与x的函数关系的是( )
A、 B、 C、 D、5. 如图,P为正六边形 边上一动点,点P从点D出发,沿六边形的边以1cm/s的速度按逆时针方向运动,运动到点C停止.设点P的运动时间为 ,以点P、C、D为顶点的三角形的面积是 ,则下列图象能大致反映y与x的函数关系的是( ) A、
A、 B、
B、 C、
C、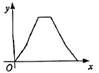 D、
D、 6. 如图,以 的三边为直角边分别向外作等腰直角三角形.若 ,则图中阴影部分的面积为( )
6. 如图,以 的三边为直角边分别向外作等腰直角三角形.若 ,则图中阴影部分的面积为( )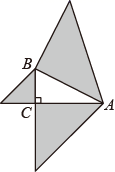 A、3 B、 C、 D、7. 如图,点B,C,E在同一直线上,且 , , ,下列结论不一定成立的是( )
A、3 B、 C、 D、7. 如图,点B,C,E在同一直线上,且 , , ,下列结论不一定成立的是( ) A、 B、 C、 D、8. 下列图形经过折叠可以围成一个棱柱的是( )A、
A、 B、 C、 D、8. 下列图形经过折叠可以围成一个棱柱的是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,在△ABC中,∠C=90°,AB=5,AC=4,则tanB的值是( )
9. 如图,在△ABC中,∠C=90°,AB=5,AC=4,则tanB的值是( ) A、 B、 C、 D、10. 如图,在OA,OB上分别截取OD,OE使OD=OE,再分别以点D、E为圆心,大于 DE长为半径作弧,两弧在∠AOB内交于点C,射线OC就是∠AOB的角平分线.理由是连结CD,CE,证△COD≌△COE得∠COD=∠COE.证△COD≌△COE的条件是( )
A、 B、 C、 D、10. 如图,在OA,OB上分别截取OD,OE使OD=OE,再分别以点D、E为圆心,大于 DE长为半径作弧,两弧在∠AOB内交于点C,射线OC就是∠AOB的角平分线.理由是连结CD,CE,证△COD≌△COE得∠COD=∠COE.证△COD≌△COE的条件是( ) A、SAS B、AAS C、ASA D、SSS
A、SAS B、AAS C、ASA D、SSS二、填空题
-
11. 等腰三角形的一边长是2cm,另一边长是4cm,则底边长为cm.12. 如图, 与 中,已知, ,请你添加一个条件(不添加字母和辅助线),使 ,你添加的条件是.
 13. 圆锥底面圆的半径为2cm,其侧面展开图的圆心角是180°,则圆锥的侧面积是 .14. 如图,在 中, , 平分 , ,点D到 的距离为5.6,则 .
13. 圆锥底面圆的半径为2cm,其侧面展开图的圆心角是180°,则圆锥的侧面积是 .14. 如图,在 中, , 平分 , ,点D到 的距离为5.6,则 . 15. 如图,点 A 、 B 、 P 是⊙ O 上的三点,若AOB =50°,则APB 的度数为 .
15. 如图,点 A 、 B 、 P 是⊙ O 上的三点,若AOB =50°,则APB 的度数为 . 16. 如图,已知一次函数y=2x+4的图象与反比例函数的图象交于A,B两点,点B的横坐标是1,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积是 .
16. 如图,已知一次函数y=2x+4的图象与反比例函数的图象交于A,B两点,点B的横坐标是1,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积是 .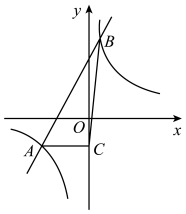
三、作图题
-
17. 如图,在直角坐标系中,将△ABC绕点A顺时针旋转90°.
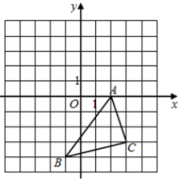 (1)、画出旋转后的△AB1C1 , 并写出B1、C1的坐标;(2)、求线段AB在旋转过程中扫过的面积.
(1)、画出旋转后的△AB1C1 , 并写出B1、C1的坐标;(2)、求线段AB在旋转过程中扫过的面积.四、解答题
-
18. 完成下面的证明
如图,点B在AG上,AGCD,CF平分∠BCD,∠ABE=∠FCB,BE⊥AF点E.
求证:∠F=90°.
证明:∵AGCD(已知)
∴∠ABC=∠BCD( ▲ )
∵∠ABE=∠FCB(已知)
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB
即∠EBC=∠FCD
∵CF平分∠BCD(已知)
∴∠BCF=∠FCD( ▲ )
∴ ▲ =∠BCF(等量代换)
∴BECF( ▲ )
∴ ▲ =∠F( ▲ )
∵BE⊥AF(已知)
∴ ▲ =90°( ▲ )
∴∠F=90°.

-


