人教版数学九年级函数专题训练
试卷更新日期:2022-03-02 类型:二轮复习
一、单选题
-
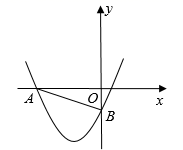
1. 已知抛物线 , 其对称轴是( )A、直线 B、直线 C、直线 D、直线2. 点 在函数 的图像上,则代数式 的值等于( )A、5 B、-3 C、3 D、-13. 若二次函数 的图象如图所示,则下列说法不正确的是( )
 A、当 时, B、当 时, 有最大值 C、图像经过点 D、当 时,4. 如图,P为正六边形 边上一动点,点P从点D出发,沿六边形的边以1cm/s的速度按逆时针方向运动,运动到点C停止.设点P的运动时间为 ,以点P、C、D为顶点的三角形的面积是 ,则下列图象能大致反映y与x的函数关系的是( )
A、当 时, B、当 时, 有最大值 C、图像经过点 D、当 时,4. 如图,P为正六边形 边上一动点,点P从点D出发,沿六边形的边以1cm/s的速度按逆时针方向运动,运动到点C停止.设点P的运动时间为 ,以点P、C、D为顶点的三角形的面积是 ,则下列图象能大致反映y与x的函数关系的是( ) A、
A、 B、
B、 C、
C、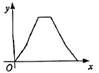 D、
D、 5. 已知反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
5. 已知反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( ) A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限6. 一次函数y=(m﹣3)x+m+2的图象经过第一、二、四象限,则m的取值范围在数轴上表示为( )A、
A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限6. 一次函数y=(m﹣3)x+m+2的图象经过第一、二、四象限,则m的取值范围在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 7. 若点A(-1, ),B(1, ),C(2, )在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,抛物线 的对称轴是直线 .下列结论:① ;② ;③ ;④ ;⑤ .其中正确结论的个数是( )
7. 若点A(-1, ),B(1, ),C(2, )在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,抛物线 的对称轴是直线 .下列结论:① ;② ;③ ;④ ;⑤ .其中正确结论的个数是( )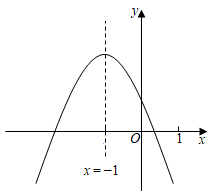 A、1个 B、2个 C、3个 D、4个9. 反比例函数y=﹣与一次函数y=x﹣2在同一坐标系中的大致图象可能是( )A、
A、1个 B、2个 C、3个 D、4个9. 反比例函数y=﹣与一次函数y=x﹣2在同一坐标系中的大致图象可能是( )A、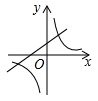 B、
B、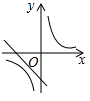 C、
C、 D、
D、 10. 二次函数 的图象 如图所示,则该函数在所给自变量的取值范围内,函数值y的取值范围是( )
10. 二次函数 的图象 如图所示,则该函数在所给自变量的取值范围内,函数值y的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 将抛物线向下平移2个单位,所得抛物线的表达式是 .12. 已知 y是关于x的一次函数,下表列出了部分对应值,则a的值为 .
x 1 2 3 y 3 a 5 13. 如图,直线y=x+2与直线y=ax+c相交于点P(m,3).则关于x的不等式x+2≥ax+c的不等式的解为 。 14. 飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是s=60t﹣12t2.飞机着陆后滑行 米才能停下来.15. 二次函数的图象与x轴有两个交点,则k的取值范围是 .16. 如图,点A在曲线到上,点B在双曲线上,ABx轴,点C是x轴上一点,连接、 , 若的面积是6,则k的值为 .
14. 飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是s=60t﹣12t2.飞机着陆后滑行 米才能停下来.15. 二次函数的图象与x轴有两个交点,则k的取值范围是 .16. 如图,点A在曲线到上,点B在双曲线上,ABx轴,点C是x轴上一点,连接、 , 若的面积是6,则k的值为 .
三、解答题
-
17. 如图,一次函数y=x+1的图像与反比例函数y的图像相交,其中一个交点的横坐标是2.求反比例函数的解析式.
 18. 如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围.
18. 如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围. 19. 如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)
19. 如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)
(1)请画出△A1B1C1 , 使△A1B1C1与△ABC关于原点对称,并写出A1、B1、C1的坐标;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2 , 并直接写出线段OB旋转到OB2扫过图形的面积.