初中数学北师大版八年级下册第五章第四节分式方程同步练习

试卷更新日期：2022-03-02 类型：同步测试

进入出卷网下载

一、单选题

1. 下列关于x的方程：① $\frac{x - 1}{2} = 5$ ，② $\frac{1}{x} = \frac{4}{x - 1}$ ，③ $\frac{1}{x} (x - 1) + x = 1$ ，④ $\frac{x}{a} = \frac{1}{b - 1}$ 中，分式方程有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
2. 解分式方程 $\frac{1}{x - 5} - 2 = \frac{3}{5 - x}$ ，去分母得（）

A、1﹣2（x﹣5）＝﹣3 B、1﹣2（x﹣5）＝3 C、1﹣2x﹣10＝﹣3 D、1﹣2x+10＝3

查看试题解析
3. 关于x的分式方程 $\frac{3}{x - a} = \frac{2}{x}$ 的解为 $x = 2$ ，则常数a的值为（）

A、-1 B、1 C、2 D、5

查看试题解析
4. 某玩具厂生产一种玩具，甲车间计划生产500个，乙车间计划生产400个，甲车间每天比乙车间多生产10个，两车间同时开始生产且同时完成任务。设乙车间每天生产x个玩具，可列方程为（）

A、 $\frac{400}{x - 10}$ = $\frac{500}{x}$ B、 $\frac{400}{x + 10}$ = $\frac{500}{x}$ C、 $\frac{400}{x}$ = $\frac{500}{x + 10}$ D、 $\frac{400}{x}$ = $\frac{500}{x - 10}$

查看试题解析
5. 分式方程 $\frac{3}{2} - \frac{1}{3 x - 1} = \frac{7}{6 x - 2}$ 的解是（）

A、 $x = \frac{2}{9}$ B、 $x = \frac{3}{4}$ C、 $x = 1$ D、 $x = \frac{4}{3}$

查看试题解析
6. 斑马线前“车让人”，不仅体现着一座城市对生命的尊重，也直接反映着城市的文明程度.如图，某路口的斑马线路段A—B—C横穿双向行驶车道，其中AB=BC=12米，在绿灯亮时，小敏共用22秒通过AC路段，其中通过BC路段的速度是通过AB路段速度的1.2倍，则小敏通过AB路段时的速度是（）

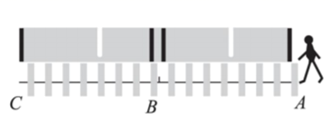A、0.5米/秒 B、1米/秒 C、1.5米/秒 D、2米/秒

查看试题解析
7. 若关于x的方程 $\frac{2}{2 - x} + \frac{x + m}{x - 2} = 2$ 有增根，则m的取值是（）

A、0 B、2 C、-2 D、1

查看试题解析
8. 若整数a使关于x的不等式组 ${\begin{array}{l} \frac{1}{2} (x - 4) + \frac{x}{2} \geq 3 \\ \frac{a - x}{4} \geq 0 \end{array}$ 无解，且使关于x的分式方程 $\frac{a x}{x - 3} + \frac{3}{3 - x} = 2$ 有整数解，那么所有满足条件的a的值的积是（）

A、2 B、3 C、 $- 3$ D、8

查看试题解析

二、填空题

9. 把分式方程 $\frac{3}{x} - \frac{x}{x + 1} = 1$ 化成整式方程，去分母后的方程为

查看试题解析
10. 分式 $\frac{x^{2} - 1}{2 (x + 1)}$ 等于零，则x的值为．

查看试题解析
11. 对于两个非零代数式，定义一种新的运算： $x@y= \frac{1}{x} + \frac{x}{y}$ .若 $x@(x-2)=1$ ，则x=.

查看试题解析
12. 某次列车平均提速vkm/h.用相同的时间，列车提速前行驶s km，提速后比提速前多行驶50 km，设提速前列车的平均速度为x km/h，则列方程为.

查看试题解析
13. 已知 $\frac{a}{a - 4} = 2 - \frac{b}{b - 4}$ ，则 $a + b$ 的值为．

查看试题解析
14. 若关于x的分式方程 $\frac{a}{x - 3} - \frac{1}{3 - x} = 2$ 有增根，则a的值为.

查看试题解析
15. 随着5月底广州“新冠”疫情的爆发，为了抵抗病毒的侵袭，量子巴川中学组织教师到社区卫生服务中心接种新冠病毒疫苗，由于疫苗数量有限，所以要分批进行接种.初中三个年级都有教师参加第一批疫苗接种，其中初一年级，初二年级和初三年级参加第一批疫苗接种的教师人数之比是5：3：2，第二批疫苗到货后，初中三个年级都有教师参加第二批疫苗接种，初三年级新增接种教师人数占总新增接种教师人数的 $\frac{2}{5}$ ，第二批疫苗接种后初三年级接种教师总人数占这三个年级接种教师总人数之和的 $\frac{8}{25}$ ，并且初一年级接种教师总人数和初二年级接种教师总人数之比为 $\frac{10}{7}$ ，则初二年级第二批接种教师人数与初中三个年级接种教师总人数之比为.

查看试题解析
16. 观察下列等式：
$\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$

将以上三个等式两边分别相加得： $\frac{1}{1 \times 2} +$ $\frac{1}{2 \times 3} +$ $\frac{1}{3 \times 4}$ = $1 - \frac{1}{2}$ + $\frac{1}{2} - \frac{1}{3}$ + $\frac{1}{3} - \frac{1}{4}$ = $1 - \frac{1}{4}$ = $\frac{3}{4}$

猜想并得出： $\frac{1}{n (n + 1)}$ = $\frac{1}{n} - \frac{1}{n + 1}$

根据以上推理，求出分式方程 $\frac{1}{x - 2} + \frac{1}{(x - 2) (x - 3)} + \frac{1}{(x - 3) (x - 4)} = 1$ 的解是．

查看试题解析

三、计算题

17. 解分式方程：

(1)、 $\frac{x^{2} - 8}{x^{2} - 4} = 1 + \frac{1}{2 - x}$ ；

(2)、 $\frac{x - 2}{x - 3} = 2 - \frac{1}{6 - 2 x}$ ．

查看试题解析

四、解答题

18. 解分式方程1- $\frac{x - 3}{2 x + 2} = \frac{3 x}{x + 1}$ 晨晨的解答如下：
解：去分母，得2x+2-x-3=6x化简得x= $- \frac{1}{5}$ ，经检验x= $- \frac{1}{5}$ 是原方程的解。

所以原方程的解是x= $- \frac{1}{5}$ 。

晨晨的解答正确吗？如果不正确，写出正确的解答。

查看试题解析
19. 列方程解应用题：
“共和国勋章”获得者，“杂交水稻之父”袁隆平院士一生致力于提高水稻的产量，为解决人类温饱问题做出了巨大贡献．某农业基地现有A，B两块试验田，A块种植普通水稻，B块种植杂交水稻．已知杂交水稻的亩产量是普通水稻亩产量的1.8倍，A块试验田种植面积比B块试验田多5亩，两块试验田的总产量都是6750千克．求杂交水稻的亩产量是多少千克？

查看试题解析
20. 若关于x的分式方程 $\frac{x}{x - 3} - 2 = \frac{m}{x - 3}$ 的解是正数，当m取最大整数时，求 $m^{2} + 2 m + 1$ 的平方根．

查看试题解析
21. 定义一种新运算“ $\otimes$ ”，规则如下： $a \otimes b = \frac{1}{a - b^{2}}$ ， $(a \neq b^{2})$ ，这里等式右边是实数运算，例如： $1 \otimes 3 = \frac{1}{1 - 3^{2}} = - \frac{1}{8}$ ．求 $x \otimes (- 2) = 1$ 中 $x$ 的值．

查看试题解析
22. 刘峰和李明相约周末去野生动物园游玩，根据他们的谈话内容，求李明乘公交车、刘峰骑自行车每小时各行多少千米？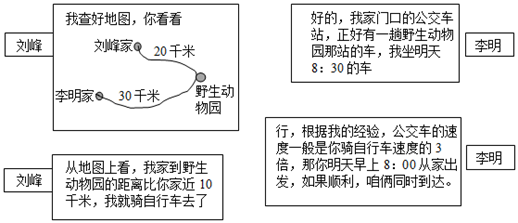

查看试题解析

五、综合题

23. 某国家5A级景区开展一年一度的旅游主题活动，活动将持续两周.景区内某餐厅今年活动期间推出“精品套餐”，在午餐和晚餐时间只出售该套餐，且定价相同.活动开始后，该套餐的销售情况如下：第一天，午餐、晚餐时间均按定价出售，当天销售总收入为30000元；第二天，午餐时间按定价共售出100份；晚餐时间按定价打九五折出售（即按定价的95%出售），当天销售总收入为37650元，且全天销售量比第一天多30%（销售量指售出的套餐的份数）.

(1)、若第一天的全天销售量为m，请用含m的代数式表示第二天晚餐时间该套餐的销售量；

(2)、该套餐的定价为多少元？

(3)、第三天，餐厅在午餐时间按定价打九二折出售该套餐，晚餐按定价出售，全天销售量比第一天多32%；第四天，午餐和晚餐时间均按定价打九折出售，全天销售量比第一天多1倍.根据该餐厅往年活动期间的销售数据，午餐时间套餐的销售量和晚餐时间套餐的销售量有如下规律：
①若套餐价格不变，则二者分别保持基本稳定；

②若套餐按定价打折，折扣相同，则二者的增长率也会大致相同.

参考前四天该套餐按定价所打折扣与销售量增长率之间的关系，若第五天午餐与晚餐时间均按定价打八八折出售该套餐，你认为全天销售量会是多少？请说明理由.

查看试题解析
24. 我们已经学过 $(x - a) (x - b) = x^{2} - (a + b) x + a b ，$ 如果关于x的分式方程满足
$x + \frac{a b}{x} = a + b$ （a，b分别为非零整数），且方程的两个跟分别为 $x_{1} = a ， x_{2} = b$ ．
我们称这样的方程为“十字方程”．
例如： $x + \frac{2}{x} = 3$ 可化为 $x + \frac{1 \times 2}{x} = 1 + 2 = 3$ ∴ $x_{1} = 1 ， x_{2} = 2$
再如： $x + \frac{6}{x} = - 5$ 可化为 $x + \frac{(- 2) \times (- 3)}{x} = - 2 - 3 = - 5$ ∴ $x_{1} = - 2 ， x_{2} = - 3$
应用上面的结论解答下列问题：

(1)、“十字方程” $x + \frac{8}{x} = - 6$ ，则 $x_{1} =$ ， $x_{2} =$ ；

(2)、“十字方程” $x - \frac{2}{x} = - 1$ 的两个解分别为 $x_{1} = a ， x_{2} = b$ ，求 $\frac{1}{a} + \frac{1}{b}$ 的值；

(3)、关于 $x$ 的“十字方程” $x + \frac{n^{2} + n}{x - 3} = 2 n + 4$ 的两个解分别为 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，求 $\frac{x_{2}}{x_{1} + 1}$ 的值．

查看试题解析

初中数学北师大版八年级下册第五章第四节 分式方程 同步练习

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

初中数学北师大版八年级下册第五章第四节分式方程同步练习