人教版数学九年级下册第二十七章第三节位似

试卷更新日期：2022-02-28 类型：同步测试

进入出卷网下载

一、单选题

1. 下列形状分别为正方形、矩形、正三角形、圆的边框，其中不一定是相似图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，已知△A′B′C′与△ABC是位似图形，点O是位似中心，若A′是OA的中点，则△A′B'C′与△ABC的面积比是（）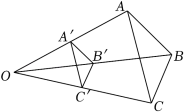

A、1：4 B、1：2 C、2：1 D、4：1

查看试题解析
3. 如图所示 $△ D E F$ 是 $△ A B C$ 位似图形的几种画法，其中正确的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
4. 如图，△ABC与△DEF位似，位似中心是点O，若OC：OF=1：3，则△ABC△DEF的周长之比是（ )

A、1：2 B、1：3 C、1：4 D、1： $\sqrt{2}$

查看试题解析
5. 如图，已知△ABC与△DEF位似，位似中心为点O，△ABC的面积与△DEF面积之比为16：9，则CO：OF的值为（）

A、3：4 B、4：7 C、4：3 D、7：4

查看试题解析
6. 如图，在平面直角坐标系中，将 $△ O A B$ 以原点O为位似中心放大后得到 $△ O C D$ ，若 $B (0 ， 1)$ ， $D (0 ， 3)$ ，则 $△ O A B$ 与 $△ O C D$ 的相似比是（）

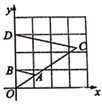A、2：1 B、1：2 C、3：1 D、1：3

查看试题解析
7. 如图，已知△OCD与△OAB是以点O为位似中心的位似图形，若C（1，2），D（3，0），B（9，0），则点A的坐标为（）

A、（2，4） B、（3，6） C、（3，5） D、（4，5）

查看试题解析
8. 下列说法中，正确的是（）

A、两个矩形必相似 B、两个含 $45 °$ 角的等腰三角形必相似 C、两个菱形必相似 D、两个含 $30 °$ 角的直角三角形必相似

查看试题解析
9. 如图，在面积为144的正方形ABCD中放两个正方形BMON和正方形DEFG，重合的小正方形OPFQ的面积为4，若点A，O，G在同一直线上，则阴影部分面积为（）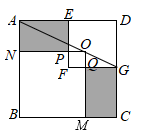

A、36 B、40 C、44 D、48

查看试题解析
10. 如图，D，E分别是△ABC的边AB，AC上的中点，如果△ADE的面积是1，则四边形BCED的面积是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 如图，在平面直角坐标系中，将△OAB以原点O为位似中心放大后得到△OCD，若B（0，1），D（0，3），则△OAB与△OCD的相似比是．

查看试题解析
12. 在平面直角坐标系 $x O y$ 中，以原点O为位似中心，作 $△ A B C$ 的位似图形，使它与 $△ A B C$ 相似比为2，若点A的坐标为 $(4 ， 2)$ ，则位似图形上与点A对应的点的坐标为．

查看试题解析
13. 如图，以点O为位似中心，将△OAB放大后得到△OCD，若OA＝3，AC＝7，则 $\frac{A B}{C D} =$ ．

查看试题解析
14. 如图，四边形ABCD与四边形EFGH位似，其位似中心为点O ，且 $\frac{O E}{E A} = \frac{4}{3}$ ，则 $\frac{F G}{B C} =$ ．

查看试题解析
15. 如果两个相似三角形对应边之比是 $4 ： 9$ ，那么它们的周长之比等于．

查看试题解析
16. 如图， $A B ∥ C D$ ， AD，BC交于点O， $\frac{A O}{O D} = \frac{1}{2}$ ．若 $B O = 3$ ，则OC的长为．

查看试题解析

三、作图题

17. 如图所示，图中的小方格都是边长为1的正方形， $△ A B C$ 与 $Δ A^{'} B^{'} C^{'}$ 是以点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上.

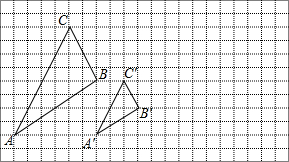
⑴画出位似中心点O；

⑵直接写出 $△ A B C$ 与 $△ A' B' C'$ 的位似比；

⑶以位似中心O为坐标原点，以格线所在直线为坐标轴建立平面直角坐标系，画出△A'B'C'关于点O中心对称的△A″B″C″，并直接写出 △A″B″C″ 各顶点的坐标.

查看试题解析

四、解答题

18. 如图， $△ A B C$ 与 $△ D E F$ 是位似图形，点O是位似中心， $O A = A D$ ， $A B = 5$ ，求DE的长.

查看试题解析
19. 如图，如果 $AC ∥ BD$ ， $CE ∥ DF$ ，那么 $△ ACE$ 与 $△ BDF$ 是否相似？ $△ ACE$ 与 $△ BDF$ 是否位似？试说明理由．

查看试题解析
20. 若AE与BD相交于点C.AC=3，BC=6，CD=10，CE=5，证明AB∥DE.

查看试题解析
21. 如图，小亮同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与树顶B在同一直线上．已知纸板的两条边EF＝30cm，DE＝40cm，延长DF交AB于点C，测得边DF离地面的高度AC＝1.5m，CD＝12m，求树高AB．

查看试题解析