山东省泰安市泰山区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，这是一个机械模具，则它的俯视图是（）

A、 B、 C、 D、

查看试题解析
2. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ，则 $s i n A + c o s A$ 的值（）．

A、大于1 B、等于1 C、小于1 D、不能确定

查看试题解析
3. 已知反比例函数 $y = - \frac{6}{x}$ ，则下列描述正确的是（）

A、图象位于第一、三象限 B、图象必经过点 $(4 ， \frac{3}{2})$ C、图象必经过点 $(4 ， - \frac{3}{2})$ D、y随x的增大而减小

查看试题解析
4. 如图， $A B C D$ 是⊙O的内接四边形，且 $∠ A B C = 125 °$ ，那么 $∠ A O C$ 等于（）

A、125° B、120° C、110° D、130°

查看试题解析
5. 如图，在直角坐标系中，点P(2，2)是一个光源．木杆AB两端的坐标分别为(0，1)，(3，1)．则木杆AB在x轴上的投影长为（）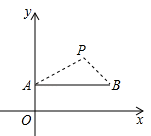

A、3 B、4 C、5 D、6

查看试题解析
6. 在一个口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机地摸出一个小球然后放回，再随机地摸出一个小球，则两次摸出的小球的标号之和等于6的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{3}{16}$

查看试题解析
7. 抛物线的函数表达式为 $y = 3 {(x - 2)}^{2} + 4$ ，若将y轴向左平移3个单位长度，将x轴向下平移3个单位长度，则该抛物线在新的平面直角坐标系中的函数表达式为（）

A、 $y = 3 {(x + 1)}^{2} + 1$ B、 $y = 3 {(x - 5)}^{2} + 1$ C、 $y = 3 {(x - 5)}^{2} + 7$ D、 $y = 3 {(x + 1)}^{2} + 7$

查看试题解析
8. 如图，在 $△ A B C$ 中， $B C = \sqrt{6} + \sqrt{2}$ ， $∠ C = 45 °$ ， $A B = \sqrt{2} A C$ ，则 $A C$ 的长为（）

A、 $\sqrt{2} + 1$ B、2 C、 $\sqrt{6}$ D、 $\sqrt{2} + \sqrt{3}$

查看试题解析
9. 函数 $y = - \frac{a}{x}$ 与 $y = a x^{2} + a$ （ $a \neq 0$ ）在同一直角坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，矩形ABCD中，G是BC的中点，过A、D、G三点的⊙O与边AB、CD分别交于点E、点F，给出下列判断：（1）AC与BD的交点是⊙O的圆心；（2）AF与DE的交点是⊙O的圆心；（3）AE=DF；（4）BC与⊙O相切，其中正确判断的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
11. 如图，已知抛物线 $y = a x^{2} + b x + c$ （ $a ， b ， c$ 为常数， $a \neq 0$ ）经过点 $(2 ， 0)$ ，且对称轴为直线 $x = \frac{1}{2}$ ，有下列结论：① $b < 0$ ；② $a + b > 0$ ；③ $4 a + 2 b + 3 c < 0$ ；④无论 $a ， b ， c$ 取何值，抛物线一定经过 $(\frac{c}{2 a} ， 0)$ ．其中正确结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 斐波那契螺旋线，也称“黄金螺旋线”，它可以通过分别以1，1，2，3，5，…为半径，依次作圆心角为90°的扇形弧线画出来（如图）．第1步中扇形的半径是1cm，按如图所示的方法依次画，第8步所画扇形的弧长为（）

A、 $4 π$ B、 $\frac{21}{2} π$ C、 $17 π$ D、 $\frac{55}{2} π$

查看试题解析

二、填空题

13. 一条上山直道的坡度为 $1 ： 3$ ，沿这条直道上山，每前进100米所上升的高度为米．

查看试题解析
14. 在一个不透明的盒子中装有2个白球，n个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是黄球的概率为 $\frac{3}{4}$ ，则n＝．

查看试题解析
15. 抛物线 $y = x^{2} - 4 x + 3$ 的顶点坐标是．

查看试题解析
16. 已知抛物线 $y_{1} = x^{2} + 2 x - 3$ 的顶点为 $A$ ，与 $x$ 轴交于点 $B$ ， $C$ （ $B$ 在 $C$ 的左边），直线 $y_{2} = k x + b$ 过 $A$ ， $B$ 两点．当 $y_{1} < y_{2}$ 时，自变量x的取值范围是．

查看试题解析
17. 如图， $A B$ 是 $⊙ O$ 的直径，点 $D$ 在 $⊙ O$ 上， $∠ D A B = 45 °$ ， $B C / / A D$ ， $C D / / A B$ ．若 $⊙ O$ 的半径为1，则图中阴影部分的面积是（结果保留 $π$ ）．

查看试题解析
18. 如图，已知等边 $△$ $O A_{1} B_{1}$ ，顶点 $A_{1}$ 在双曲线 $y = \frac{\sqrt{3}}{x} (x > 0)$ 上，点 $B_{1}$ 的坐标为 $(2 ， 0)$ ．过 $B_{1}$ 作 $B_{1} A_{2} ∥ O A_{1}$ 交双曲线于点 $A_{2}$ ，过 $A_{2}$ 作 $A_{2} B_{2} ∥ A_{1} B_{1}$ 交 $x$ 轴于点 $B_{2}$ ，得到第二个等边 $△$ $B_{1} A_{2} B_{2}$ ；过 $B_{2}$ 作 $B_{2} A_{3} ∥ B_{1} A_{2}$ 交双曲线于点 $A_{3}$ ，过 $A_{3}$ 作 $A_{3} B_{3} ∥ A_{2} B_{2}$ 交 $x$ 轴于点 $B_{3}$ ，得到第三个等边 $△$ $B_{2} A_{3} B_{3}$ ；以此类推，…，则点 $B_{12}$ 的坐标为．

查看试题解析

三、解答题

19. 为了更好地解决养老问题，某服务中心引入优质社会资源为甲，乙两个社区共30名老人提供居家养老服务，收集得到这30名老人的年龄（单位：岁）如下：
甲社区
68
69
73
75
76
78
80
82
83
84
85
85
90
92
95
乙社区
67
69
72
74
75
78
80
81
85
85
88
89
91
96
98
根据以上信息解答下列问题：

(1)、求甲社区老人年龄的中位数和众数；

(2)、现从两个社区年龄在70岁以下的4名老人中随机抽取2名了解居家养老服务情况，求这2名老人恰好来自同一个社区的概率．

查看试题解析
20. 一辆汽车匀速通过某段公路，所需时间t（h）与行驶速度v（km/h）满足函数关系： $t = \frac{k}{v}$ ，其图象为如图所示的一段曲线且端点为A(40，1)和B(m，0.5)．

(1)、求k和m的值；

(2)、若行驶速度不得超过50km/h，则汽车通过该路段最少需要多少时间？

查看试题解析
21. 如图，1号楼在2号楼的南侧，两楼高度均为 $90 m$ ，楼间距为 $A B$ ．冬至日正午，太阳光线与水平面所成的角为30°，1号楼在2号楼墙面上的影高为 $C A$ ；春分日正午，太阳光线与水平面所成的角为60°，1号楼在2号楼墙面上的影高为 $D A$ ．已知 $C D = 56 m$ ．

(1)、求楼间距 $A B$ ；

(2)、若2号楼共30层，层高均为 $3 m$ ，则点 $C$ 位于第几层？

查看试题解析
22. 一座隧道的截面由抛物线和长方形构成，长方形的长为8m，宽为2m，隧道最高点P位于AB的中央且距地面6m，建立如图所示的坐标系．

(1)、求抛物线的表达式；

(2)、一辆货车高4m，宽2.4m，能否从该隧道内通过，为什么？

查看试题解析
23. 如图，⊙O是 $△$ ABC的外接圆，∠ABC=45°，OC $∥$ AD，AD交BC的延长线于D，AB交OC于E．

(1)、求证：AD是⊙O的切线；

(2)、若AE= $2 \sqrt{5}$ ， CE=2，求⊙O的半径和线段BC的长．

查看试题解析
24. 如图，一次函数 $y = k_{1} x + b$ 的图象与反比例函数 $y = \frac{k_{2}}{x}$ 的图象相交于A、B两点，其中点A的坐标为(-1，4)，点B的坐标为(4，n)．

(1)、求这两个函数的表达式；

(2)、点P在线段AB上，且 $S_{△ A O P} ： {S_{△}}_{B O P} = 1 ： 2$ ，求点P的坐标．

查看试题解析
25. 如图，抛物线 $y = \frac{2}{3} x^{2} + b x + c$ 与x轴交于A，B两点，与y轴交于C点，连接AC，已知B(﹣1，0)，且抛物线经过点D(2，﹣2)．

(1)、求抛物线的表达式；

(2)、若点E是抛物线上第四象限内的一点，且 $S_{△ A B E} = 2$ ，求点E的坐标；

(3)、若点P是y轴上一点，以P，A，C三点为顶点的三角形是等腰三角形，求P点的坐标．

查看试题解析

甲社区	68	69	73	75	76	78	80	82	83	84	85	85	90	92	95
乙社区	67	69	72	74	75	78	80	81	85	85	88	89	91	96	98