山东省青岛市崂山区2021-2022学年九年级上学期期末数学试题
试卷更新日期：2022-02-28 类型：期末考试
一、单选题
-
1. 如图所示圆柱的左视图是（ ）
A、
B、
C、
D、
2. 在同一时刻，身高1.6米的小强在阳光下的影长为0.8米，一棵大树的影长为4.8米，则树的高度为（ ）A、2.4米 B、4.8米 C、9.6米 D、12.8米3. 2021年上半年我国成功发射了天和核心舱、天舟二号货运飞船和神舟十二号载人飞船，中国的太空经济时代即将到来．太空基金会发布新闻稿指出，2018年的全球航天经济总量为80亿美元，2020年全球航天经济总量再创新高，达到3850亿美元，假设2018年到2020年每年的平均增长率为x，则可列方程为（ ）A、80(1+x)＝3850 B、80x＝3850 C、80(1+x)3＝3850 D、80(1+x)2＝38504. 已知点(﹣2，y1)，(1，y2)，(3，y3)和(2，3)都在反比例函数y＝的图象上，那么y1 ， y2 ， y3的大小关系是（ ）A、y1＜y2＜y3 B、y3＜y2＜y1 C、y2＜y1＜y3 D、y1＜y3＜y25. 如图，点A，B，C在⊙O上，∠ACB=54°，则∠ABO的度数是（ ）
A、27° B、36° C、54° D、108°6. 如图，在△ABC中，点E，D，F分别在边AB，BC，CA上，且DE∥CA，DF∥BA.下列四个判断：①四边形AEDF是平行四边形；②如果∠BAC＝90°，那么四边形AEDF是矩形；③如果AD平分∠BAC，那么四边形AEDF是菱形；④如果AD⊥BC且AB＝AC，那么四边形AEDF是菱形.正确的个数是（ ）
A、4 B、3 C、2 D、17. 如图，在矩形ABCD中，AD=2，AB=1，以A为圆心，AD的长为半径画弧交BC于点E，则图中空白部分的面积是（ ）
A、1﹣ B、2﹣ C、 D、2+8. 函数y＝ax2+bx+c（a≠0），如果a＞b＞c且a+b+c＝0，则它的图象可能是（ ）A、
B、
C、
D、
二、填空题
-
9. tan30°= ．10. 一个不透明的盒子中装有8个白球和若干个红球，它们除颜色不同外，其余均相同，从盒子中随机摸出一球记下其颜色，再把它放回盒子中摇匀，重复上述过程，共试验1000次，其中有199次摸到红球，由此估计盒子中的红球大约有个．11. 已知二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示，则关于x的一元二次方程ax2+bx+c＝0的解为 ．
12. 如图，在▱ABCD中，AB=6，AD=8，∠ADC的平分线交BC于点F，交AB的延长线于点G，过点C作CE⊥DG，垂足为E，CE=2，则△BFG的周长为 ．
13. 写出一组a，b的值，使二次函数y＝ax2+bx+2的图象与x轴有两个不同的交点，则a，b的值可以是a＝ ， b＝ ．14. 如图，函数y＝和y＝﹣的图象分别是l1和l2 ． 设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则△PAB的面积为 ．
三、解答题
-
15. 求作：Rt△ABC，使∠A＝45°，斜边AB＝a．
16. 解方程：(1)、4x(2x+1)＝3(2x+1)；(2)、﹣3x2+4x+4＝0．17. 甲、乙两同学只有一张乒乓球比赛的门票，谁都想去，最后商定通过转盘游戏决定，游戏规则是：转动下面平均分成三个扇形且标有不同颜色的转盘，转盘连续转动两次，若指针前后所指颜色相同，则甲去；否则乙去．（如果指针恰好停在分割线上，那么重转一次，直到指针指向一种颜色为止）．你认为这个游戏公平吗？请说明理由．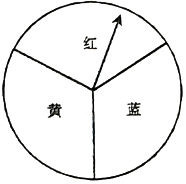
18. 青岛电视塔座落于样林公园内的太平山上，为测得电视塔的高度，如图所示，某同学在某栋楼的底部点D处看向电视塔底端的点B处，测得仰角是45°，在楼顶点E处，看向电视塔顶端C处，测得仰角是64°，已知楼高DE的高度为112米，AD⊥AC，DE∥AC，太平山的高度AB约为120米，求青岛电视塔BC的高度．（tan64°≈2）
19. 如图，点A(1，m)，B(6，n)在反比例函数图象上，AD⊥y轴于点D，BC⊥y轴于点C，DC=5．
(1)、求m，n的值并写出反比例函数的表达式；(2)、连结AB，在线段DC上是否存在一点P，使△PAB的面积等于10？若存在，求出P点坐标；若不存在，请说明理由．20. 小颖同学想用“描点法”画二次函数y＝ax2+bx+c（a≠0）的图象，取自变量x的6个值，分别计算出对应的y值，如表：x
……
﹣2
﹣1
0
1
2
3
……
y
……
11
2
﹣1
2
5
m
……
由于粗心，小颖算错了其中的一个y值．
(1)、求该二次函数表达式；(2)、请你指出这个算错的y值；(3)、通过计算求m的值．21. 如图，在▱ABCD中，AC⊥CD．
(1)、延长DC到E，使CE=CD，连接BE，求证：四边形ABEC是矩形；(2)、若点F，G分别是BC，AD的中点，连接AF，CG，试判断四边形AFCG是什么特殊的四边形？并证明你的结论．22. 2021年10月28日，青岛市崂山区启动了古树名木普查工作，期间对全区古树名木进行健康生长状况、立地条件，保护措施等调查，崂山区共有古树名木300多株，现知树龄最大的古树距今已有2100余年．崂山区王哥庄街道港东社区的一株银杏树，树龄已400余年，社区现在想借助如图所示的互相垂直的两面墙（墙体足够长），在墙角区域用50m长的篱笆围成一个矩形保护区域来保护这株银杏树，设AB=xm．（AB≤AD）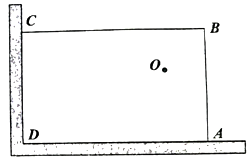
(1)、若围成保护区域的面积为600m2 ， 求x的值；(2)、已知这株银杏树在点O处，且与墙体AD的距离为10m，与墙体CD的距离为18m．如果在围建矩形保护区域时，将银杏树围在花园内（含边界上，树的粗细忽略不计），那么能围成的矩形的最大面积是多少？23. 实际问题：某学校共有18个教学班（每班的学生都多于10人）．为了解学生课余时间上网情况，学校打算做一次抽样调查，如果要确保全校抽取出来的学生中至少有10人在同一班级，那么全校最少需抽取多少名学生？建立模型：为解决上面的“实际问题”，我们先建立并研究下面从口袋中摸球的数学模型：在不透明的口袋中装有红、黄、白、……m种颜色的小球若干个（除颜色外完全相同），现要确保从口袋中随机模出的小球至少有n个是同色的，则最少需摸出多少个小球？
为了找到解决问题的办法，我们可把上述问题简单化．
(1)、探究一：我们研究一个口袋中装有红、黄、白3种颜色的小球若干个（除颜色外完全相同），现要确保从口袋中随机摸出的小球至少有n个是同色的，则最少需摸出多少个小球？⑴我们首先考虑最简单的情况：即要确保从装有红、黄、白3种颜色的口袋中摸出小球，至少有2个是同色的，则最少需摸出多少个小球？
假若从袋中随机摸出3个小球，它们的颜色可能会出现多种情况，其中最不利的情况就是它们的颜色各不相同，那么只需再从发中摸出1个小球就可确保至少有2个小球同色，即最少需摸出小球的个数是：1+3=4（如图①）；
⑵要确保从装有红、黄、白3种颜色的口袋中摸出小球，至少有3个是同色的，则最少需摸出多少个小球？
我们只需在（1）的基础上，再从袋中摸出3个小球，就可确保至少有3个小球同色，即最少．需摸出小球的个数是：1+3×2=7（如图②）
⑶要确保从装有红、黄、白3种颜色的口袋中摸出小球，至少有4个是同色的，则最少需摸出多少个小球？
我们只需在（2）的基础上，再从袋中摸出3个小球，就可确保至少有4个小球同色，即最少需摸出小球的个数是：1+3×3=10（如图③）；
……
⑷要确保从装有红、黄、白3种颜色的口袋中摸出小球，至少有10个是同色的，则最少需摸出多少个小球？最少需摸出小球的个数是；
⑸要确保从装有红、黄、白3种颜色的口袋中摸出小球，至少有n个是同色的，则最少需摸出个小球．
(2)、探究二：我们研究一个口袋中装有红、黄、白黑4种颜色的小球若干个（除颜色外完全相同），现要确保从口袋中随机摸出的小球至少有n个是同色的，则最少需摸出多少个小球？⑹我们首先考虑最简单的情况：即要确保从装有红、黄、白、黑4种颜色的口袋中摸出小球，至少有2个是同色的，则最少需摸出个小球；
⑺要确保从装有红、黄、白、黑4种颜色的口袋中摸出小球，至少有3个是同色的，则最少需摸出个小球；
⑻要确保从装有红、黄、白黑4种颜色的口袋中摸出小球，至少有4个是同色的，则最少需摸出个小球；
⑼要确保从装有红、黄、白、黑4种颜色的口袋中摸出小球，至少有n个是同色的，则最少需摸出个小球；
(3)、探究三：⑽在不透明的口袋中装有红、黄、白、蓝、绿5种颜色的小球若干个（除颜色外完全相同），现从袋中随机摸球：若要确保摸出的小球至少有n个同色，则最少需摸出小球的个数是 ．(4)、探究四：⑾在不透明口袋中装有m种颜色的小球若干个（除颜色外完全相同），现从袋中随机摸球：若要确保摸出的小球至少有n个同色，则最少需摸出小球的个数是；(5)、问题解决：⑿根据上述探究过程中建立的数学模型，求出全校最少需抽取名学生．24. 如图所示，在△ABC中，∠C=30°，BC=20，AC=16，E为BC中点．动点P从点B出发，沿BE方向匀速运动，速度为每秒1个单位长度；同时，点Q从点C出发，沿CE方向匀速运动，速度为每秒1个单位长度，当一个点停止移动时，另一个点也立即停止移动．过点P作PD//AC，交AB于D，连接DQ，设点P运动的时间为t（s）．（0<t<10）
(1)、当t＝3时，求PD的长；(2)、设△DPQ面积为y，求y关于t的函数关系式；(3)、是否存在某一时刻t，使S△DPQ：S△ABC＝3：25？若存在，请求出t的值；如果不存在，请说明理由．