山东省济南市章丘区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
1. 如图,一个水晶球摆件,它是由一个长方体和一个球体组成的几何体,则其主视图是( )
 A、
A、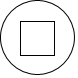 B、
B、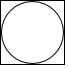 C、
C、 D、
D、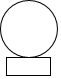 2. 已知 , 则下列比例式成立的是( )A、 B、 C、 D、3. 反比例函数的图象经过点(﹣2,3),则此函数的图象也经过点( )A、(2,﹣3) B、(﹣3,﹣3) C、(2,3) D、(﹣4,6)4. 如图,△ABC中,点D、E分别为边AB和AC中点,且S△ADE=3,则S△ABC等于( )
2. 已知 , 则下列比例式成立的是( )A、 B、 C、 D、3. 反比例函数的图象经过点(﹣2,3),则此函数的图象也经过点( )A、(2,﹣3) B、(﹣3,﹣3) C、(2,3) D、(﹣4,6)4. 如图,△ABC中,点D、E分别为边AB和AC中点,且S△ADE=3,则S△ABC等于( ) A、4 B、8 C、9 D、125. 在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球,通过多次摸球试验后,发现摸到白球的频率约为30%,估计袋中黑球有( )个.A、8 B、9 C、14 D、156. 已知点A(﹣1,y1)、B(﹣3,y2)、C( ,y3)在反比例函数y=﹣ 的图象上,则y1、y2、y3的大小关系正确的是( )A、y1>y2>y3 B、y2>y1>y3 C、y2>y3>y1 D、y3>y1>y27. 关于x的方程x²+mx+6=0的一个根为-2,则另一个根是( )A、-3 B、-6 C、3 D、68. 下列命题正确的是( )A、对角线相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的平行四边形是菱形 D、对角线互相垂直且相等的四边形是正方形9. 已知关于x的方程 , 则下列关于该方程根的判断,正确的是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、不能确定10. 在同一平面直角坐标系中,函数y=kx+k与y=(k≠0)的图象可能是( )A、
A、4 B、8 C、9 D、125. 在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球,通过多次摸球试验后,发现摸到白球的频率约为30%,估计袋中黑球有( )个.A、8 B、9 C、14 D、156. 已知点A(﹣1,y1)、B(﹣3,y2)、C( ,y3)在反比例函数y=﹣ 的图象上,则y1、y2、y3的大小关系正确的是( )A、y1>y2>y3 B、y2>y1>y3 C、y2>y3>y1 D、y3>y1>y27. 关于x的方程x²+mx+6=0的一个根为-2,则另一个根是( )A、-3 B、-6 C、3 D、68. 下列命题正确的是( )A、对角线相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的平行四边形是菱形 D、对角线互相垂直且相等的四边形是正方形9. 已知关于x的方程 , 则下列关于该方程根的判断,正确的是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、不能确定10. 在同一平面直角坐标系中,函数y=kx+k与y=(k≠0)的图象可能是( )A、 B、
B、 C、
C、 D、
D、 11. 如图,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( )cm.
11. 如图,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( )cm. A、 B、5 C、 D、812. 如图,中, , , , , 为 , 边上的两个动点,且 , 为中点,则的最小值为( )
A、 B、5 C、 D、812. 如图,中, , , , , 为 , 边上的两个动点,且 , 为中点,则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 一个布袋里装有2个只有颜色不同的球,其中1个红球,1个白球,从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则两次摸到的球恰好颜色不同的概率是 .14. 如图,是小莹设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD, . 且测得米,米,PD=12米,那么该古墙的高度是米.
 15. 如图,在菱形ABCD中,已知AB=5,AC=6,那么菱形ABCD的面积为 .
15. 如图,在菱形ABCD中,已知AB=5,AC=6,那么菱形ABCD的面积为 . 16. 某商品经过两次连续提价,每件售价由原来的100元上涨到了121元.设平均每次涨价的百分率为x,则x是 .17. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,已知AD=5,BD=4,那么BC= .
16. 某商品经过两次连续提价,每件售价由原来的100元上涨到了121元.设平均每次涨价的百分率为x,则x是 .17. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,已知AD=5,BD=4,那么BC= . 18. 如图,点 在反比例函数 的图象上,点 在 轴上,且 ,直线 与双曲线 交于点 , ,则 的坐标是 .
18. 如图,点 在反比例函数 的图象上,点 在 轴上,且 ,直线 与双曲线 交于点 , ,则 的坐标是 .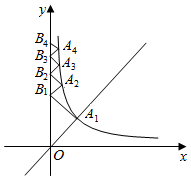
三、解答题
-
19. 解方程:20. 已知:如图,、分别是的边、上的点, , , , . 求的长度.
 21. 如图,四边形ACMF、BCNE 是两个正方形.求证:AN=BM .
21. 如图,四边形ACMF、BCNE 是两个正方形.求证:AN=BM . 22. 如图,学校打算用16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图,墙长9m),面积是30m2 . 求生物园的长和宽.
22. 如图,学校打算用16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图,墙长9m),面积是30m2 . 求生物园的长和宽. 23. 如图,在四边形 中, ,对角线 的垂直平分线与边 、 分别相交于点 、 .
23. 如图,在四边形 中, ,对角线 的垂直平分线与边 、 分别相交于点 、 .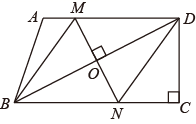 (1)、求证:四边形 是菱形;(2)、若 , , ,求菱形 的周长.24. 某学校为了解全校学生对电视节目(新闻、体育、动画、娱乐、戏曲)的喜爱情况,从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
(1)、求证:四边形 是菱形;(2)、若 , , ,求菱形 的周长.24. 某学校为了解全校学生对电视节目(新闻、体育、动画、娱乐、戏曲)的喜爱情况,从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.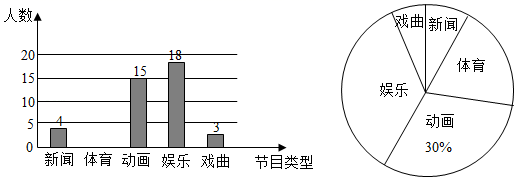
请根据以上信息,解答下列问题
(1)、这次被调查的学生共有多少名?(2)、请将条形统计图补充完整;(3)、若该校有3000名学生,估计全校学生中喜欢体育节目的约有多少名?(4)、该校宣传部需要宣传干事,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,用树状图或列表法求恰好选中甲、乙两位同学的概率.25. 如图 (1)、感知:数学课上,老师给出了一个模型:
(1)、感知:数学课上,老师给出了一个模型:如图1, , 由 , , 可得 ;又因为 , 可得 , 进而得到 . 我们把这个模型称为“一线三等角”模型.
(2)、应用:实战组受此模型的启发,将三等角变为非直角,如图2,在中, , , 点P是BC边上的一个动点(不与B、C重合),点D是AC边上的一个动点,且 .①求证:;
②当点P为BC中点时,求CD的长;
(3)、拓展:在(2)的条件下如图2,当为等腰三角形时,请直接写出BP的长.26. 如图,已知一次函数图象y=x+b与y轴交于点C(0,1),与反比例函数图象y=交于点A(a,2)和点B两点. (1)、求一次函数和反比例函数的解析式;(2)、求点B的坐标和△AOB的面积;(3)、若点M为y轴上的一个动点,N为平面内一个动点,当以A、B、M、N为顶点的四边形是矩形时,请求出M点坐标.27. 如图1,在Rt△ABC中,∠BAC=90°,∠ACB=60°,AC=2,点A1 , B1为边AC,BC的中点,连接A1B1 , 将△A1B1C绕点C逆时针旋转α(0°≤α≤360°).
(1)、求一次函数和反比例函数的解析式;(2)、求点B的坐标和△AOB的面积;(3)、若点M为y轴上的一个动点,N为平面内一个动点,当以A、B、M、N为顶点的四边形是矩形时,请求出M点坐标.27. 如图1,在Rt△ABC中,∠BAC=90°,∠ACB=60°,AC=2,点A1 , B1为边AC,BC的中点,连接A1B1 , 将△A1B1C绕点C逆时针旋转α(0°≤α≤360°).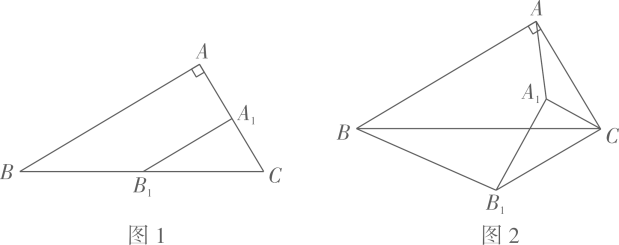 (1)、如图1,当α=0°时, , BB1 , AA1所在直线相交所成的较小夹角的度数为;(2)、将△A1B1C绕点C逆时针旋转至图2所示位置时,(1)中结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(3)、当△A1B1C绕点C逆时针旋转过程中,
(1)、如图1,当α=0°时, , BB1 , AA1所在直线相交所成的较小夹角的度数为;(2)、将△A1B1C绕点C逆时针旋转至图2所示位置时,(1)中结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(3)、当△A1B1C绕点C逆时针旋转过程中,①请直接写出△ABA1面积的最大值;
②当A1 , B1 , B三点共线时,请直接写出线段BB1的长.