山东省济南市平阴县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
1. 如图所示的物体,其主视图是( )
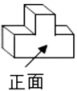 A、
A、 B、
B、 C、
C、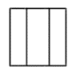 D、
D、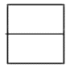 2. 一元二次方程 的解是( )A、 B、 C、 , D、 ,3. 反比例函数是y= 的图象在( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限4. 在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、12个 B、14个 C、16个 D、18个5. 抛物线y=(x-4) 2-3的顶点坐标是( )A、(-4,3) B、(-4,-3) C、(4,3) D、(4,-3)6. 关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是( )A、 B、 C、 D、 且7. 如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=35°,则∠AOB的度数为( )
2. 一元二次方程 的解是( )A、 B、 C、 , D、 ,3. 反比例函数是y= 的图象在( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限4. 在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、12个 B、14个 C、16个 D、18个5. 抛物线y=(x-4) 2-3的顶点坐标是( )A、(-4,3) B、(-4,-3) C、(4,3) D、(4,-3)6. 关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是( )A、 B、 C、 D、 且7. 如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=35°,则∠AOB的度数为( )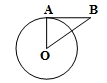 A、65° B、55° C、45° D、35°8. 如图,△ABC的顶点都是正方形网格中的格点,则sin∠ABC等于( )
A、65° B、55° C、45° D、35°8. 如图,△ABC的顶点都是正方形网格中的格点,则sin∠ABC等于( )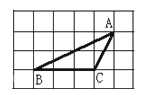 A、 B、 C、 D、9. 函数先向右平移2个单位,再向下平移2个单位,所得函数解析式是( )A、 B、 C、 D、10. 如图, 和 是以点 为位似中心的位似三角形,若 为 的中点, ,则 的面积为( )
A、 B、 C、 D、9. 函数先向右平移2个单位,再向下平移2个单位,所得函数解析式是( )A、 B、 C、 D、10. 如图, 和 是以点 为位似中心的位似三角形,若 为 的中点, ,则 的面积为( )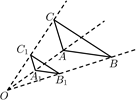 A、15 B、12 C、9 D、611. 已知二次函数的图象如图所示,下列结论中正确的是( )
A、15 B、12 C、9 D、611. 已知二次函数的图象如图所示,下列结论中正确的是( )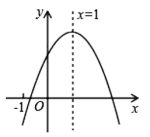 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
12. 电影《我和我的祖国》讲述了普通人与国家之间息息相关密不可分的动人故事,一上映就获得全国人民的追捧,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若把增长率记作x,则方程不能列为( )A、3(1+x)=10 B、3(1+x)2=10 C、3+3(1+x)2=10 D、3+3(1+x)+3(1+x)2=10
三、填空题
-
13. 若
14. 利用标杆 测量建筑物的高度的示意图如图所示,若标杆 的高为 米,测得 米, 米,则建筑物的高 为米.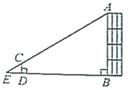 15. 如图,点A,B,C是⊙O上的点,OA=AB,则∠C的度数为 .
15. 如图,点A,B,C是⊙O上的点,OA=AB,则∠C的度数为 . 16. 如图是某商场自动扶梯的示意图,自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A、C之间的距离为6m,则自动扶梯的垂直高度BD=m.(结果保留根号).
16. 如图是某商场自动扶梯的示意图,自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A、C之间的距离为6m,则自动扶梯的垂直高度BD=m.(结果保留根号).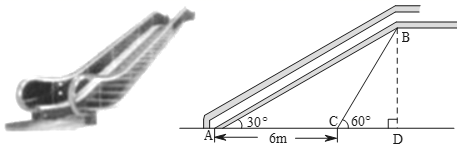 17. 如图,矩形ABCD中,AB=1,AD= .以A为圆心,AD的长为半径做弧交BC边于点E , 则图中 的弧长是.
17. 如图,矩形ABCD中,AB=1,AD= .以A为圆心,AD的长为半径做弧交BC边于点E , 则图中 的弧长是.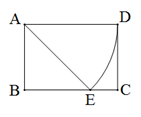 18. 如图,在平面直角坐标系中,四边形的边与x轴的正半轴重合, , 轴,对角线交于点M.已知 , 的面积为4.若反比例函数的图象恰好经过点M,则k的值为 .
18. 如图,在平面直角坐标系中,四边形的边与x轴的正半轴重合, , 轴,对角线交于点M.已知 , 的面积为4.若反比例函数的图象恰好经过点M,则k的值为 .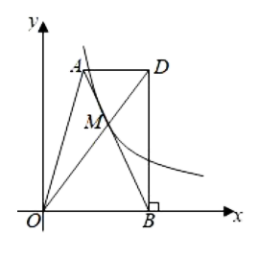
四、解答题
-
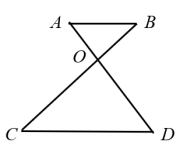
19. 计算:(1)、(2)、20. 如图, , 、相交于点O,若 , , . 求的长度.
 21. 如图,连接A市和B市的高速公路是高速和BC高速,现在要修一条新高速AB,在施工过程中,决定在A、B两地开凿隧道,从而将两地间的公路进行改建.汽车原来从A地到B地需途经C地沿折线行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知千米, , , 开通隧道后,汽车从A地到B地要走多少千米?(结果保留根号)
21. 如图,连接A市和B市的高速公路是高速和BC高速,现在要修一条新高速AB,在施工过程中,决定在A、B两地开凿隧道,从而将两地间的公路进行改建.汽车原来从A地到B地需途经C地沿折线行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知千米, , , 开通隧道后,汽车从A地到B地要走多少千米?(结果保留根号)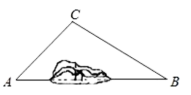 22. 如图,在△ABC中,AB=AC,∠BAC=120°,点D在BC边上, D经过点A和点B且与BC边相交于点E.
22. 如图,在△ABC中,AB=AC,∠BAC=120°,点D在BC边上, D经过点A和点B且与BC边相交于点E. (1)、求证:AC是 D的切线.(2)、若CE= ,求 D的半径.23. 一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.(1)、摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为.(2)、摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.24. 某校劳动教育课上,老师让同学们设计劳动基地的规划.如图,在块长、宽的矩形空地上,修建两条同样宽的相互垂直的道路,剩余部分栽种绿植,要使栽种面积为 , 则修建的路宽应为多少米?
(1)、求证:AC是 D的切线.(2)、若CE= ,求 D的半径.23. 一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.(1)、摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为.(2)、摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.24. 某校劳动教育课上,老师让同学们设计劳动基地的规划.如图,在块长、宽的矩形空地上,修建两条同样宽的相互垂直的道路,剩余部分栽种绿植,要使栽种面积为 , 则修建的路宽应为多少米?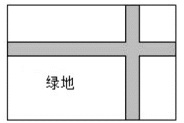 25. 如图,一次函数的图象与反比例函数的图象分别交于点和点 , 与y轴交于点C.
25. 如图,一次函数的图象与反比例函数的图象分别交于点和点 , 与y轴交于点C.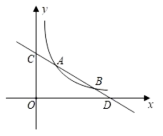 (1)、请直接写出m的值;(2)、求直线AB的解析式;(3)、观察图象,直接写出不等式的解集.26. 如图1,在中, , , , 点D、E分别是边BC、的中点,连接DE.将绕点C逆时针方向旋转,记旋转角为 .
(1)、请直接写出m的值;(2)、求直线AB的解析式;(3)、观察图象,直接写出不等式的解集.26. 如图1,在中, , , , 点D、E分别是边BC、的中点,连接DE.将绕点C逆时针方向旋转,记旋转角为 .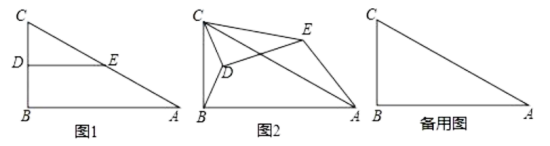 (1)、问题发现
(1)、问题发现①当时,;②当时, .
(2)、拓展探究试判断:当时,的大小有无变化?请仅就图2的情形给出证明.
(3)、问题解决绕点C逆时针旋转至A、B、E三点在同一条直线上时,请直接写出线段BD的长 .
27. 如图,抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,-3).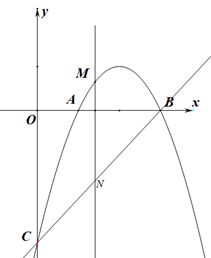 (1)、求抛物线的解析式;(2)、若点M是抛物线在x轴上方的部分上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值.(3)、在(2)的条件下,当MN取最大值时,在抛物线的对称轴上是否存在点P,使 是等腰三角形?若存在,请求出所有点P的坐标,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若点M是抛物线在x轴上方的部分上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值.(3)、在(2)的条件下,当MN取最大值时,在抛物线的对称轴上是否存在点P,使 是等腰三角形?若存在,请求出所有点P的坐标,若不存在,请说明理由.
-