山东省济南市商河县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 有一个铁制零件（正方体中间挖去一个圆柱形孔）如图放置，它的左视图是（）

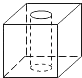A、 B、 C、 D、

查看试题解析
2. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $B C = 3$ ，则 $s i n A$ 的值为（）

A、 $\frac{5}{3}$ B、 $\frac{4}{5}$ C、 $\frac{5}{4}$ D、 $\frac{3}{5}$

查看试题解析
3. 小明和小华玩“石头、剪子、布”的游戏．若随机出手一次，则小华获胜的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{2}{9}$ D、 $\frac{1}{2}$

查看试题解析
4. 如图，在同一时刻，身高1.6米的小丽在阳光下的影长为2.5米，一棵大树的影长为5米，则这棵树的高度为（）

A、7.8米 B、3.2米 C、2.30米 D、1.5米

查看试题解析
5. 一元二次方程 $x^{2} - 2 x + 3 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
6. 若反比例函数 $y = - \frac{2}{x}$ 的图象上有两点A(−2，m)，B(−1，n)，则m，n的关系是（）

A、 $m > n$ B、m＜n C、m=n D、无法确定

查看试题解析
7. 如图，正方形ABCD的边长为7，在各边上顺次截取 $A E = B F = C G = D H = 4$ ，则四边形EFGH的面积为（）．

A、20 B、25 C、30 D、35

查看试题解析
8. 二次函数 $y = 2 (x - 4)^{2} + 5$ 的开口方向、对称轴、顶点坐标分别是（）

A、向下、直线x= $- 4$ 、（ $- 4$ ， 5） B、向上、直线x= $- 4$ 、（ $- 4$ ， 5） C、向上、直线x=4、（4， $- 5$ ） D、向上、直线x=4、（4，5）

查看试题解析
9. 已知矩形ABCD的周长为20cm，两条对角线AC，BD相交于点O，过点O作AC的垂线EF，分别交两边AD，BC于E，F（不与顶点重合），则以下关于△CDE与△ABF判断完全正确的一项为（）

A、△CDE与△ABF的周长都等于10cm，但面积不一定相等 B、△CDE与△ABF全等，且周长都为10cm C、△CDE与△ABF全等，且周长都为5cm D、△CDE与△ABF全等，但它们的周长和面积都不能确定

查看试题解析
10. 如图，小强从热气球上的A点测量一栋高楼顶部的仰角 $∠ D A B = 30 °$ ，测量这栋高楼底部的俯角 $∠ D A C = 60 °$ ，热气球与高楼的水平距离为 $A D = 15 \sqrt{3}$ 米，则这栋高楼的高BC为（）米．

A、45 B、60 C、75 D、90

查看试题解析
11. 如图，点 $A$ 的坐标是 $(2 ， 0) ， Δ A B O$ 是等边三角形，点 $B$ 在第一象限．若反比例函数 $y = \frac{k}{x}$ 的图象经过点 $B$ ，则 $k$ 的值是（）

A、 $1$ B、 $2$ C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图象如图所示，图象过点 $(- 1 ， 0)$ ，对称轴为直线x＝1，下列结论：① $a b c ＜ 0$ ；② $b ＜ c$ ；③ $3 a + c = 0$ ；④当 $y ＞ 0$ 时， $- 1 ＜ x ＜ 3$ 其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 已知： $\frac{x}{y} = \frac{3}{2} (y \neq 0)$ ，则 $\frac{x}{x + y} =$ ．

查看试题解析
14. 如图，在正方形网格中，四边形ABCD为菱形，则 $t a n \frac{∠ B A D}{2}$ 等于．

查看试题解析
15. 若关于x的方程 $x^{2} + m x - 8 = 0$ 有一个根是2，则另一个根为．

查看试题解析
16. 两个相似多边形的周长之比为2，面积之比为m，则m为．

查看试题解析
17. 如图，在平面直角坐标系中，过点 $M (- 3 ， 2)$ 分别作x轴、y轴的垂线与反比例函数 $y = \frac{4}{x}$ 的图象交于A，B两点，则四边形MAOB的面积为．

查看试题解析
18. 矩形纸片ABCD中， $A B = 5$ ， $A D = 4$ ，将纸片折叠，使点B落在边CD上的 $B^{^{'}}$ 处，折痕为AE．延长 $B^{^{'}} E$ 交AB的延长线于M，折痕AE上有点P，下列五个结论中正确的是．
① $∠ M = ∠ D A B^{'}$ ；② $P B = P B^{'}$ ；③ $A E = \frac{5 \sqrt{5}}{2}$ ；④ $M B^{'} = C D$ ；⑤若 $B^{'} P ⊥ C D$ ，则 $E B^{'} = B^{'} P$ ．

查看试题解析

三、解答题

19. 计算： ${(- 1)}^{4} - 2 c o s 60 ° + t a n 45 ° - {(\sqrt{3} - \sqrt{2})}^{0}$ ．

查看试题解析
20. 如图，在菱形ABCD中，点E，F分别是边AB和BC上的点，且BE＝BF．求证：∠DEF＝∠DFE．

查看试题解析
21. 在一个不透明的盒子里，装有四个分别标有数字1、2、3、4的小球，它们的形状、大小、质地等完全相同，小明先从盒子里随机取出一个小球，记下数字为x，放回盒子摇匀后，再由小华随机取出一个小球，记下数字为y．请用列表法或画树状图法求出点（x，y）落在反比例函数 $y = \frac{4}{x}$ 的图象上的概率．

查看试题解析
22. 如图，已知点C、D在线段AB上，且AC=4，BD=9，△PCD是边长为6的等边三角形．

(1)、求证：△PAC∽△BPD；

(2)、求∠APB的度数．

查看试题解析
23. 一种竹制躺椅如图①所示，其侧面示意图如图②③所示，这种躺椅可以通过改变支撑杆CD的位置来调节躺椅舒适度，假设AB所在的直线为地面，已知 $A E = 120 c m$ ，当把图②中的支撑杆CD调节至图③中的 $C D'$ 的位置时， $∠ E A B$ 由 $20 °$ 变为 $25 °$ ．

(1)、你能求出调节后该躺椅的枕部E到地面的高度增加了多少吗？（参考数据： $s i n 20 ° \approx 0.34$ ， $s i n 25 ° \approx 0.42$ ）

(2)、已知点O为AE的一个三等分点，根据人体工程学，当点O到地面的距离为26cm时，人体感觉最舒适．请你求出此时枕部E到地面的高度．

查看试题解析
24. 工人师傅用一块长为10dm，宽为6dm的矩形铁皮制作一个无盖的长方体容器，需要将四角各裁掉一个正方形，（厚度不计）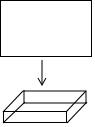

(1)、在图中画出裁剪示意图，用实线表示裁剪线，虚线表示折痕；

(2)、并求长方体底面面积为12dm²时，裁掉的正方形边长多大？

查看试题解析
25. 如图，一次函数 $y = k_{1} x + b$ 的图象与反比例函数 $y = \frac{k_{2}}{x}$ 的图象相交于A、B两点，其中点A的坐标为 $(- 1 ， 4)$ ，点B的坐标为 $(4 ， n)$ ．

(1)、求这两个函数的表达式：

(2)、根据图象，直接写出满足 $k_{1} x + b > \frac{k_{2}}{x}$ 的x的取值范围；

(3)、连接OA，OB，求 $△ A O B$ 的面积；

(4)、点P在线段AB上，且 $S_{△ A O P} ： S_{△ B O P} = 1 ： 2$ ，求点P的坐标．

查看试题解析
26. 如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．易证：CE＝CF．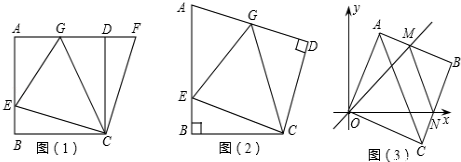

(1)、在图1中，若G在AD上，且∠GCE＝45°．试猜想GE，BE，GD三线段之间的数量关系，并证明你的结论．

(2)、运用（1）中解答所积累的经验和知识，完成下面两题：
①如图2，在四边形ABCD中∠B＝∠D＝90°，BC＝CD，点E，点G分别是AB边，AD边上的动点．若∠BCD＝α，∠ECG＝β，试探索当α和β满足什么关系时，图1中GE，BE，GD三线段之间的关系仍然成立，并说明理由．
②在平面直角坐标中，边长为1的正方形OABC的两顶点A，C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y＝x上时停止旋转，旋转过程中，AB边交直线y＝x于点M，BC边交x轴于点N（如图3）．设△MBN的周长为p，在旋转正方形OABC的过程中，p值是否有变化？若不变，请直接写出结论．

查看试题解析
27. 如图，在平面直角坐标系中，二次函数 $y = x^{2} + b x + c$ 的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于 $C (0 ， - 3)$ 点，点P是直线BC下方的抛物线上一动点．

(1)、求这个二次函数的表达式．

(2)、连结PO、PC，并把 $△ P O C$ 沿CO翻折，得到四边形 $P O P C$ ，那么是否存在点P，使四边形 $P O P C$ 为菱形？若存在，请求出此时点P的坐标；若不存在请说明理由．

(3)、当点P运动到什么位置时，四边形ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积．

查看试题解析