山东省济南市历下区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
1. 如果 , 那么的值是( )A、 B、 C、 D、2. 下列几何体中,其三视图的三个视图完全相同的是( )A、
 B、
B、 C、
C、 D、
D、 3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 如图,A , B , C是⊙O上的三点,若 ,则 的度数是( )
3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 如图,A , B , C是⊙O上的三点,若 ,则 的度数是( ) A、40° B、35° C、30° D、25°5. 如图,河坝横断面迎水坡的坡比为 , 坝高为4m,则的长度为( )
A、40° B、35° C、30° D、25°5. 如图,河坝横断面迎水坡的坡比为 , 坝高为4m,则的长度为( )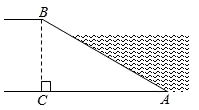 A、8m B、m C、m D、m6. 如果⊙O的半径为6,线段OP的长为3,则点P与⊙O的位置关系是( )A、点P在⊙O上 B、点P在⊙O内 C、点P在⊙O外 D、无法确定7. 关于反比例函数的图象性质,下列说法不正确的是( )A、图象经过点 B、图象位于第一、三象限 C、当时,随的增大而增大 D、图象关于原点成中心对称8. 如图,在下列方格纸中的四个三角形,是相似三角形的是( )
A、8m B、m C、m D、m6. 如果⊙O的半径为6,线段OP的长为3,则点P与⊙O的位置关系是( )A、点P在⊙O上 B、点P在⊙O内 C、点P在⊙O外 D、无法确定7. 关于反比例函数的图象性质,下列说法不正确的是( )A、图象经过点 B、图象位于第一、三象限 C、当时,随的增大而增大 D、图象关于原点成中心对称8. 如图,在下列方格纸中的四个三角形,是相似三角形的是( )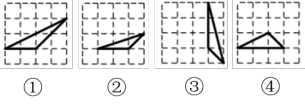 A、①和② B、①和③ C、②和③ D、②和④9. 已知抛物线 ,a是常数,且 ,下列选项中可能是它大致图像的是( )A、
A、①和② B、①和③ C、②和③ D、②和④9. 已知抛物线 ,a是常数,且 ,下列选项中可能是它大致图像的是( )A、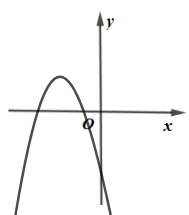 B、
B、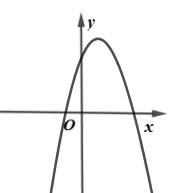 C、
C、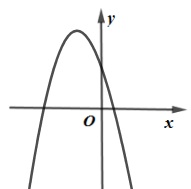 D、
D、 10. 我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°,A与P两点的距离为10千米;它沿铅垂线上升到达B处时,此时在P处测得B点的仰角∠DPB为45°,则天舟二号从A处到B处的距离AB的长为( )(参考数据: , )
10. 我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°,A与P两点的距离为10千米;它沿铅垂线上升到达B处时,此时在P处测得B点的仰角∠DPB为45°,则天舟二号从A处到B处的距离AB的长为( )(参考数据: , )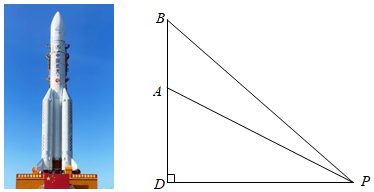 A、2.0千米 B、1.5千米 C、2.5千米 D、3.5千米11. 有一张矩形纸片ABCD,已知AB=2 , AD=4,上面有一个以AD为直径的半圆(如图1),E为边AB上一点,将纸片沿DE折叠,A点恰好落在BC上,此时半圆还露在外面的部分(如图2,阴影部分)的面积是( )
A、2.0千米 B、1.5千米 C、2.5千米 D、3.5千米11. 有一张矩形纸片ABCD,已知AB=2 , AD=4,上面有一个以AD为直径的半圆(如图1),E为边AB上一点,将纸片沿DE折叠,A点恰好落在BC上,此时半圆还露在外面的部分(如图2,阴影部分)的面积是( )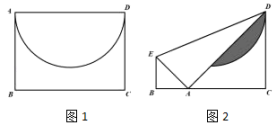 A、 B、 C、 D、12. 新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数(为常数)在的图像上存在两个二倍点,则的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、12. 新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数(为常数)在的图像上存在两个二倍点,则的取值范围是( )A、 B、 C、 D、二、填空题
-
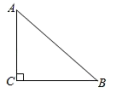
13. 如图,在中, , , , 则 .
 14. 为了估计水塘中的鱼数,养鱼者先从鱼塘中捕获50条鱼,在每一条鱼身上做好标记后把这些鱼放归鱼塘,再从鱼塘中打捞鱼.通过多次实验后发现捕捞的鱼中有作记号的频率稳定在2.5%左右,则鱼塘中估计有鱼条.15. 如图,在圆内接正六边形ABCDEF中,半径OA=4,则这个正六边形的边长为 .
14. 为了估计水塘中的鱼数,养鱼者先从鱼塘中捕获50条鱼,在每一条鱼身上做好标记后把这些鱼放归鱼塘,再从鱼塘中打捞鱼.通过多次实验后发现捕捞的鱼中有作记号的频率稳定在2.5%左右,则鱼塘中估计有鱼条.15. 如图,在圆内接正六边形ABCDEF中,半径OA=4,则这个正六边形的边长为 .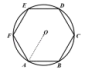 16. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的方程ax2+bx+c=0(a≠0)的解为 .
16. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的方程ax2+bx+c=0(a≠0)的解为 .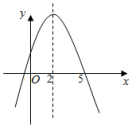 17. 如图,矩形ABCD的顶点A、B分别在反比例函数与的图象上,点C、D在x轴上,AB、BD分别交y轴于点E、F,则阴影部分的面积为 .
17. 如图,矩形ABCD的顶点A、B分别在反比例函数与的图象上,点C、D在x轴上,AB、BD分别交y轴于点E、F,则阴影部分的面积为 .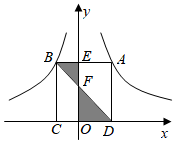 18. 在菱形中, , , , 相交于点 . 将一个足够大的直角三角板60°角的顶点放在菱形的顶点处,绕点左右旋转,其中三角板60°角的两边分别与边 , 相交于点 , , 连接与相交于点 . 旋转过程中,当点为边的四等分点时(), .
18. 在菱形中, , , , 相交于点 . 将一个足够大的直角三角板60°角的顶点放在菱形的顶点处,绕点左右旋转,其中三角板60°角的两边分别与边 , 相交于点 , , 连接与相交于点 . 旋转过程中,当点为边的四等分点时(), .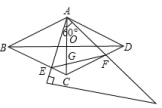
三、解答题
-
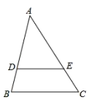
19. 计算:20. 如图,在中,、在边、上, , , , , 求的长度.
 21. 如图,某飞机于空中处探测到目标 , 此时飞行高度m,从飞机上看地平面指挥台的俯角 . 求飞机与指挥台的距离.【参考数据: , , 】.
21. 如图,某飞机于空中处探测到目标 , 此时飞行高度m,从飞机上看地平面指挥台的俯角 . 求飞机与指挥台的距离.【参考数据: , , 】.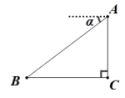 22. 20届年级组董老师为学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.
22. 20届年级组董老师为学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.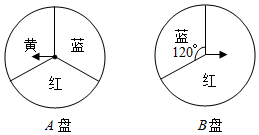 (1)、若小蕊同学转动一次A盘,求出她转出红色的概率;(2)、若小津同学同时转动A盘和B盘,请通过列表或者树状图的方式,求出她赢得游戏的概率.23. 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
(1)、若小蕊同学转动一次A盘,求出她转出红色的概率;(2)、若小津同学同时转动A盘和B盘,请通过列表或者树状图的方式,求出她赢得游戏的概率.23. 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.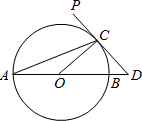 (1)、求∠D的度数;(2)、若CD=1,求BD的长.24. 如图,用一段长36米的篱笆,围成一个矩形花圃,花圃的一边靠墙(墙足够长),设AB边的长为x米,矩形ABCD的面积为S平方米.
(1)、求∠D的度数;(2)、若CD=1,求BD的长.24. 如图,用一段长36米的篱笆,围成一个矩形花圃,花圃的一边靠墙(墙足够长),设AB边的长为x米,矩形ABCD的面积为S平方米.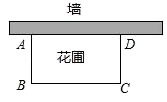 (1)、求与之间的函数关系式,并写出自变量的取值范围;(2)、当为何值时,有最大值?并求出最大值.25. 如图,在平面直角坐标系中,O为坐标原点,点A坐标为(3,0),四边形OABC为平行四边形,反比例函数y=(x>0)的图象经过点C,与边AB交于点D,若OC=2 , tan∠AOC=1.
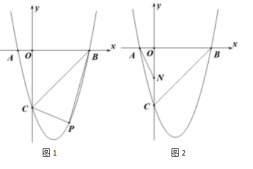
(1)、求与之间的函数关系式,并写出自变量的取值范围;(2)、当为何值时,有最大值?并求出最大值.25. 如图,在平面直角坐标系中,O为坐标原点,点A坐标为(3,0),四边形OABC为平行四边形,反比例函数y=(x>0)的图象经过点C,与边AB交于点D,若OC=2 , tan∠AOC=1.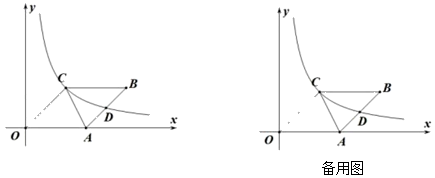 (1)、求反比例函数解析式;(2)、点P(a,0)是x轴上一动点,求|PC-PD|最大时a的值;(3)、连接CA,在反比例函数图象上是否存在点M,平面内是否存在点N,使得四边形CAMN为矩形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)、求反比例函数解析式;(2)、点P(a,0)是x轴上一动点,求|PC-PD|最大时a的值;(3)、连接CA,在反比例函数图象上是否存在点M,平面内是否存在点N,使得四边形CAMN为矩形,若存在,请直接写出点M的坐标;若不存在,请说明理由.